��Ŀ����
11��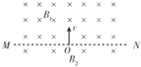 ��ͼ��ʾ����MNΪ�������ǿ�ų����������ֱֽ�����MN�߽��Ϸ��ĴŸ�Ӧǿ��B1�����·��ĴŸ�Ӧǿ��B2����B2=B0��һ����Ϊm����������ҵ���Ϊq�����Ӵ�O����ͼʾ����ֱMN����ų�B1�У���������������
��ͼ��ʾ����MNΪ�������ǿ�ų����������ֱֽ�����MN�߽��Ϸ��ĴŸ�Ӧǿ��B1�����·��ĴŸ�Ӧǿ��B2����B2=B0��һ����Ϊm����������ҵ���Ϊq�����Ӵ�O����ͼʾ����ֱMN����ų�B1�У�����������������1����B1=2B0����������Ӵ�O��������ٴλص�O�������ʱ�䣬�����������˶��켣��
��2����������Ӵ�O����������ٴλص�O�������B1�Ŀ���ֵ�����˶��������õ�ʱ�䣮
���� ��1�����������ִų���ֻ������������������Բ���˶�������ţ�ٵڶ����ɿ�֪�뾶${R}_{1}=\frac{1}{2}{R}_{2}$���������ֶ�����������ת�������켣�����ݹ켣ȷ��ʱ�������ڵĹ�ϵ����������������»ص�O���ʱ�䣻
��2�����������ڴų���������Բ���˶������˶��켣�������������˶����ص㣬�ҳ��뾶��Ĺ�ϵ�������������B1����ֵ�Ͷ�Ӧ���˶�ʱ�䣻
��� �⣺��1���������ڴų�B1��B2��Բ���˶��İ뾶�ֱ�ΪR1��R2��
�����ڴų���������Բ���˶�����ţ�ٵڶ����ɣ�$qvB=m\frac{{v}^{2}}{R}$��
��ã�${R}_{1}=\frac{mv}{q{B}_{1}}$��${R}_{2}=\frac{mv}{q{B}_{2}}$��
��B1=2B0=2B2ʱ��${R}_{1}=\frac{1}{2}{R}_{2}$��
�������ֶ����жϿ���֪���������ڴų�B1������ʱ�뷽����ת���ڴų�B2����˳ʱ�뷽����ת��
���������˶��켣��ͼ����ʾ��

ͼ��
�����ڴų�����Բ���˶������ڣ�$T=\frac{2��R}{v}=\frac{2��m}{qB}$��
�����˶���ʱ��Ӧ���������֣����ϰ�ų���2�������ڣ����°�ų��İ�����ڣ�
�������Ӵ�O��������ٴλص�O�������ʱ��Ϊ��
${t}_{1}={T}_{1}+\frac{{T}_{2}}{2}=\frac{2��m}{2q{B}_{0}}+\frac{1}{2}��\frac{2��m}{q{B}_{2}}=\frac{2��m}{q{B}_{0}}$
��2���������������˶��Ĺ켣��ͼ����ʾ��
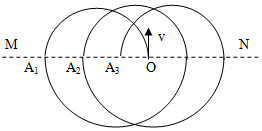
ͼ��
��A1A2=��x�����x=2R2-2R1��
����һ�λص�O��ʱӦ���㣺n��x=2R1��
��ã�$\frac{{R}_{1}}{{R}_{2}}=\frac{n}{n+1}$��
��$R=\frac{mv}{qB}$�ã�$B=\frac{mv}{qR}$��
����$\frac{{B}_{1}}{{B}_{2}}=\frac{n+1}{n}$��
�ʣ�${B}_{1}=\frac{n+1}{n}{B}_{0}$��n=1��2��3������
�����˶��켣����MN�Ϸ���B1�ų����У�n+1������Բ���˶�ʱ�䣺${t}_{1}=\frac{1}{2}��n+1��{T}_{1}=\frac{n+1}{2}•\frac{2��m}{q{B}_{1}}=\frac{n��m}{q{B}_{0}}$
��MN�·���B2�ų�����n����Բ���˶�ʱ�䣺${t}_{2}=\frac{n}{2}{T}_{2}=\frac{n}{2}•\frac{2��m}{q{B}_{0}}=\frac{n��m}{q{B}_{0}}$
��������Ӵ�O����������ٴλص�O����˶�ʱ�䣺
$t={t}_{1}+{t}_{2}=\frac{2n��m}{q{B}_{0}}$��n=1��2��3������
�𣺣�1���������Ӵ�O��������ٴλص�O�������ʱ��$t=\frac{2��m}{q{B}_{0}}$���˶��켣��ͼ�ף�
��2�������������ٴλص�O���B1��ֵΪ${B}_{1}=\frac{n+1}{n}{B}_{0}$��n=1��2��3������
�������Ӵ�O����������ٴλص�O����˶�ʱ��Ϊ$t=\frac{2n��m}{q{B}_{0}}$��n=1��2��3������
���� ���⿼�����������������ͬ�ų�����������Բ���˶������⣬�ۺϿ�����������ڴų�����Բ���˶������֪ʶ�����ֶ���ȷ�����˶��켣ͼ�ǽ������Ĺؼ������еڶ��ʲ���Ҫ����ȷ�����˶��켣������Ҫ���˶��켣���ҳ��˶��Ĺ��ɣ�������Ҫ��ϸߣ�

 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�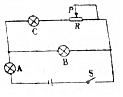 ����ͼ��ʾ�ĵ�·�У�A��B��CΪ������ȫ��ͬ��С���ݣ�RΪ��������������������ͷλ��ͼ����ʾ��λ��ʱ���պϿ��أ�����С���ݾ��ܷ��⣮�ڻ�����ͷ���һ����Ĺ����У�����������ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У�A��B��CΪ������ȫ��ͬ��С���ݣ�RΪ��������������������ͷλ��ͼ����ʾ��λ��ʱ���պϿ��أ�����С���ݾ��ܷ��⣮�ڻ�����ͷ���һ����Ĺ����У�����������ȷ���ǣ�������| A�� | С����A���� | B�� | С����B�䰵 | ||
| C�� | С����C�䰵 | D�� | ����С���ݶ����� |
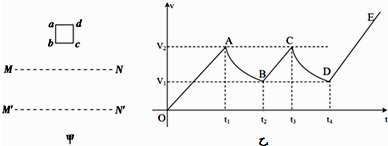
| A�� | t2���߿�ȫ������ų�˲�䣬t4���߿�ȫ���뿪�ų�˲�� | |
| B�� | ��bc�߽���ų���һֱ��ad���뿪�ų�Ϊֹ����Ӧ���������Ĺ�ΪmgS | |
| C�� | v1�Ĵ�С����Ϊ$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D�� | �߿��ų������������߿�����ĵ�������߿����ų�����������������ĵ������ |
| ������Ƥ���¶˵Ĺ������ | ��Ƥ���¶˵����꣨X/mm�� | |
| �� | �� | |
| 1 | 216.5 | 216.5 |
| 2 | 246.7 | 232.0 |
| 3 | 284.0 | 246.5 |
| 4 | 335.0 | 264.2 |
| 5 | 394.5 | 281.3 |
| 6 | 462.0 | 301.0 |
��2����ͬѧ�����ݸ�����ʵ��Ҫ���ң���
 ��ͼ��ʾ����̨��������һ��ֱ��$\frac{1}{4}$Բ���ι⻬������뾶R=$\frac{5}{4}$m������˵�B������ˮƽ������M=5kg�Ľ������飨����Ϊ�ʵ㣩�ɹ������A�ɾ�ֹ�ͷţ��뿪B���ʱ��t=1sײ����б���ϵ�P�㣮��֪б�����Ǧ�=37�㣬б���C��B���ˮƽ����x0=3m��gȡ10m/s2��sin37��=0.6��cos37��=0.8�����ƿ���������
��ͼ��ʾ����̨��������һ��ֱ��$\frac{1}{4}$Բ���ι⻬������뾶R=$\frac{5}{4}$m������˵�B������ˮƽ������M=5kg�Ľ������飨����Ϊ�ʵ㣩�ɹ������A�ɾ�ֹ�ͷţ��뿪B���ʱ��t=1sײ����б���ϵ�P�㣮��֪б�����Ǧ�=37�㣬б���C��B���ˮƽ����x0=3m��gȡ10m/s2��sin37��=0.6��cos37��=0.8�����ƿ���������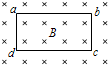 ��ͼ��ʾ����ǿ�ų�����һ���αպ���Ȧabcd����Ȧƽ����ų���ֱ����֪��Ȧ������N=100���߳�ab=1.0m��bc=0.5m������r=5�����Ÿ�Ӧǿ��B��0��1s�ڴ�����ȱ仯��0.3T�� ��1��5s�ڴ�0.3T���ȱ仯��-0.3T��ȡ��ֱֽ������Ϊ�ų�����������
��ͼ��ʾ����ǿ�ų�����һ���αպ���Ȧabcd����Ȧƽ����ų���ֱ����֪��Ȧ������N=100���߳�ab=1.0m��bc=0.5m������r=5�����Ÿ�Ӧǿ��B��0��1s�ڴ�����ȱ仯��0.3T�� ��1��5s�ڴ�0.3T���ȱ仯��-0.3T��ȡ��ֱֽ������Ϊ�ų�����������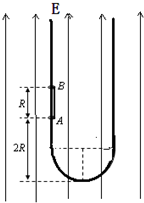 �⻬��Ե�ij������״��ͼ��ʾ���ײ�Ϊ��Բ�ͣ��뾶R���̶�����ֱƽ���ڣ�A��B��������Ϊm��С����A������Ϊ-2q��B�Ĵ�����Ϊ+q���ó�ΪR�ľ�Ե���������һ�����ڹ���ϣ�����װ�÷��ڵ糡ǿ��ΪE=$\frac{mg}{3q}$��������ֱ���ϵ���ǿ�糡�У���AB������ͼʾλ�þ�ֹ�ͷţ�A���뿪�ײ�2R����������˺���ĽӴ���Ҳ������A��B��Ŀ��������ã���
�⻬��Ե�ij������״��ͼ��ʾ���ײ�Ϊ��Բ�ͣ��뾶R���̶�����ֱƽ���ڣ�A��B��������Ϊm��С����A������Ϊ-2q��B�Ĵ�����Ϊ+q���ó�ΪR�ľ�Ե���������һ�����ڹ���ϣ�����װ�÷��ڵ糡ǿ��ΪE=$\frac{mg}{3q}$��������ֱ���ϵ���ǿ�糡�У���AB������ͼʾλ�þ�ֹ�ͷţ�A���뿪�ײ�2R����������˺���ĽӴ���Ҳ������A��B��Ŀ��������ã���