��Ŀ����
16��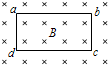 ��ͼ��ʾ����ǿ�ų�����һ���αպ���Ȧabcd����Ȧƽ����ų���ֱ����֪��Ȧ������N=100���߳�ab=1.0m��bc=0.5m������r=5�����Ÿ�Ӧǿ��B��0��1s�ڴ�����ȱ仯��0.3T�� ��1��5s�ڴ�0.3T���ȱ仯��-0.3T��ȡ��ֱֽ������Ϊ�ų�����������
��ͼ��ʾ����ǿ�ų�����һ���αպ���Ȧabcd����Ȧƽ����ų���ֱ����֪��Ȧ������N=100���߳�ab=1.0m��bc=0.5m������r=5�����Ÿ�Ӧǿ��B��0��1s�ڴ�����ȱ仯��0.3T�� ��1��5s�ڴ�0.3T���ȱ仯��-0.3T��ȡ��ֱֽ������Ϊ�ų�������������1��0.5sʱ��Ȧ�ڸ�Ӧ�綯�ƵĴ�СE��Ӧ�����ķ���
��2����1��5s��ͨ����Ȧ�ĵ����q��
���� ��1�������ȷ���Ÿ�Ӧǿ��B�ı仯��$\frac{��B}{��t}$�����ݷ����ڵ�Ÿ�Ӧ���������Ӧ�綯�ƣ�������ζ����жϸ�Ӧ�����ķ���
��2���ɷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɺ͵����Ķ���ʽI=$\frac{q}{t}$ �����������
��� �⣺��1����0��1s�ڣ��Ÿ�Ӧǿ��B�ı仯��Ϊ��$\frac{��B}{��t}$=$\frac{0.3-0}{1}$T/s=0.3T/s��
���ڴ�ͨ�����ȱ仯����0��1s����Ȧ�в����ĸ�Ӧ�綯�ƺ㶨���䣬����ݷ����ڵ�Ÿ�Ӧ���ɵã�0.5sʱ��Ȧ�ڸ�Ӧ�綯�ƵĴ�СΪ��
E1=N$\frac{��∅}{��t}$=N��$\frac{��B}{��t}$����ab��bc=100��0.3��1��0.5=15V
������ζ����жϵ�֪����Ȧ�и�Ӧ����Ϊ��ʱ�뷽��
��2����1��5s�ڣ��Ÿ�Ӧǿ��B�ı仯�ʴ�СΪ��
$\frac{��B��}{��t��}$=$\frac{0.3-��-0.3��}{4}$��T/s��=0.15T/s��
���ڴ�ͨ�����ȱ仯����1��5s����Ȧ�в����ĸ�Ӧ�綯�ƺ㶨���䣬����ݷ����ڵ�Ÿ�Ӧ���ɵ�1��5sʱ��Ȧ�ڸ�Ӧ�綯�ƵĴ�СΪ��
E2=N$\frac{��∅}{��t}$=N$\frac{��B}{��t}$��ab��bc=100��0.15��1��0.5=7.5V
ͨ����Ȧ�ĵ����Ϊ��q=I2t2=��$\frac{E}{R}$����t2=��$\frac{7.5}{5}$����4C=6C��
�𣺣�1��0.5sʱ��Ȧ�ڸ�Ӧ�綯�ƵĴ�СEΪ15V����Ӧ����Ϊ��ʱ�뷽��
��2����1��5s��ͨ����Ȧ�ĵ����qΪ6C��
���� �����Ƿ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɡ��������ɺ���ζ��ɵ�֪ʶ���ۺ�Ӧ�ã���Щ���ǵ�Ÿ�Ӧ�������صĻ������ɣ�Ҫ�������գ�������ȷӦ�ã�

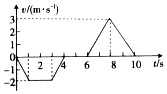
| A�� | ������DZ��������Ϊ6m | |
| B�� | ȫ�����У���DZˮ�����ߵ������ٶ���1.5m/s2 | |
| C�� | 0��6sʱ���ڣ�DZˮ������ƽ���ٶȴ�СΪ1.5m/s | |
| D�� | 0һ10sʱ���ڣ�DZˮ�����ߵ�ƽ���ٶ�Ϊ�� |
 ��ͼ��ʾ�ĵ�·�У��պϿ���S�����������Ļ�ƬP�����ƶ�һС�ξ��������˵������ȷ���ǣ�������
��ͼ��ʾ�ĵ�·�У��պϿ���S�����������Ļ�ƬP�����ƶ�һС�ξ��������˵������ȷ���ǣ�������| A�� | ������ʾ������ | B�� | ��ѹ��ʾ����С | ||
| C�� | ��Դ���ܹ������� | D�� | R0�Ĺ��ʼ�С |
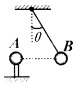 ��ͼ��ʾ��һ������˿���¶˵� �������С��B��ֹ��ͼʾλ�ã��̶��Ĵ�����ɵ�A������ΪQ��B������Ϊm�������Ϊq����=30�㣬A��B��ͬһˮƽ���ϣ�����װ�ô�������У���A��B�����ľ��룮
��ͼ��ʾ��һ������˿���¶˵� �������С��B��ֹ��ͼʾλ�ã��̶��Ĵ�����ɵ�A������ΪQ��B������Ϊm�������Ϊq����=30�㣬A��B��ͬһˮƽ���ϣ�����װ�ô�������У���A��B�����ľ��룮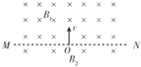 ��ͼ��ʾ����MNΪ�������ǿ�ų����������ֱֽ�����MN�߽��Ϸ��ĴŸ�Ӧǿ��B1�����·��ĴŸ�Ӧǿ��B2����B2=B0��һ����Ϊm����������ҵ���Ϊq�����Ӵ�O����ͼʾ����ֱMN����ų�B1�У���������������
��ͼ��ʾ����MNΪ�������ǿ�ų����������ֱֽ�����MN�߽��Ϸ��ĴŸ�Ӧǿ��B1�����·��ĴŸ�Ӧǿ��B2����B2=B0��һ����Ϊm����������ҵ���Ϊq�����Ӵ�O����ͼʾ����ֱMN����ų�B1�У���������������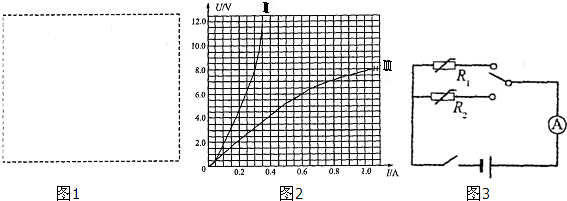
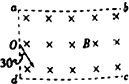 һ�㹻���ľ�������abcd�ڳ����Ÿ�Ӧǿ��ΪB������ֱֽ���������ǿ�ų��������������߽�ad��ΪL���ִ�ad�е�O��ֱ�ڴų�����һ�ٶȷ�����ad�н�Ϊ30�㡢��СΪv0�Ĵ��������ӣ���ͼ��ʾ����֪���ӵ����Ϊq������Ϊm���������ƣ�����Ҫ�������ܴ�ab������ų���v0Ӧ����ʲô������
һ�㹻���ľ�������abcd�ڳ����Ÿ�Ӧǿ��ΪB������ֱֽ���������ǿ�ų��������������߽�ad��ΪL���ִ�ad�е�O��ֱ�ڴų�����һ�ٶȷ�����ad�н�Ϊ30�㡢��СΪv0�Ĵ��������ӣ���ͼ��ʾ����֪���ӵ����Ϊq������Ϊm���������ƣ�����Ҫ�������ܴ�ab������ų���v0Ӧ����ʲô������