题目内容
7. 小球下落一段距离后,落在竖立的弹簧上,弹簧被压缩的过程中.
小球下落一段距离后,落在竖立的弹簧上,弹簧被压缩的过程中.(1)都有哪些力对小球做功?这些力分别做什么功?
(2)上述过程中,动能如何变化?重力势能如何变化?
(3)动能与重力势能的总和守恒吗?系统的机械能守恒吗?以上过程不计空气阻力.
分析 (1)分析小球的受力情况,根据力与位移方向间的关系,判断做功正负.
(2)根据受力情况分析小球的运动情况,从而判断动能的变化.根据高度变化可以确认重力势能的变化.
(3)忽略空气阻力,小球和弹簧组成的系统机械能守恒,根据弹性势能与弹簧形变量的关系可以判断弹性势能的变化,从而判断动能和重力势能总和的变化.
解答 解:(1)重力和弹簧的弹力对小球做功,重力做正功,弹力做负功.
(2)开始于弹簧接触时,压缩量较小,因此开始阶段,弹簧对小球向上的弹力小于向下重力,此时合外力方向向下,小球加速下降.随着压缩量的增加,弹力增大,当合外力为零时速度最大,由于惯性物体继续向下运动,此时合外力方向向上,物体减速,所以速度先增大后减小,则动能先增大后减小.
重力一直做正功,则重力势能一直减小.
(3)对于小球和弹簧组成的系统,只有重力和弹力做功,系统的机械能守恒,由于弹性势能不断增大,所以小球的动能与重力势能的总和不断减小.
答:
(1)重力和弹簧的弹力对小球做功,重力做正功,弹力做负功.
(2)动能先增大后减小.重力势能一直减小.
(3)系统的机械能守恒,小球的动能与重力势能的总和不断减小.
点评 本题关键要能正确分析小球的运动情况,运用机械能守恒的条件进行分析,要注意小球的机械能不守恒.

练习册系列答案
相关题目
17.质量为m的跳水运动员,从离地面高H的跳台上以速度v1斜向上跳起,跳起最大高度离跳台为h,最后以速度v2进入水中,空气阻力不能忽略,则下列说法正确的是( )
| A. | 运动员起跳时做的功为$\frac{1}{2}$mv${\;}_{1}^{2}$ | |
| B. | 从起跳到入水,重力对运动员做的功为mgH | |
| C. | 运动员克服空气阻力做的功为mg(H+h)-$\frac{1}{2}$mv${\;}_{2}^{2}$ | |
| D. | 运动员在下落过程中机械能总量保持不变 |
15. 如图所示,实线表示电场线,虚线表示带电粒子只在电场力作用下的运动轨迹,a,b为其运动轨迹上的两点,可以判定( )
如图所示,实线表示电场线,虚线表示带电粒子只在电场力作用下的运动轨迹,a,b为其运动轨迹上的两点,可以判定( )
 如图所示,实线表示电场线,虚线表示带电粒子只在电场力作用下的运动轨迹,a,b为其运动轨迹上的两点,可以判定( )
如图所示,实线表示电场线,虚线表示带电粒子只在电场力作用下的运动轨迹,a,b为其运动轨迹上的两点,可以判定( )| A. | 粒子在a点的速度大于在b点的速度 | |
| B. | 粒子在a点的加速度大于在b点的加速度 | |
| C. | 粒子一定带正电荷 | |
| D. | 粒子在a点电势能大于在b点的电势能 |
2.2014年9月29日,在仁川亚运会跳高比赛中,卡塔尔选手穆•巴沙姆打破亚运会32年跳高记录,夺得金牌.假设穆•巴沙姆的重心离地面高1.2m,起跳后身体横着越过了1.96m的高度.据此可估算出他起跳时的竖直速度大约为(取g=10m/s2)( )
| A. | 2m/s | B. | 4m/s | C. | 6m/s | D. | 8m/s |
12.一物体受到两个力F1和F2,它们之间的夹角为θ,则( )
| A. | 若θ为锐角,保持F1不变而使F2减小,则合力减小 | |
| B. | 若θ为钝角,保持F1不变而使F2减小,则合力减小 | |
| C. | 若θ为钝角,保持F1不变而使F2减小,则合力增大 | |
| D. | 若保持F1和F2不变而使θ减小,则合力一定增大 |
7.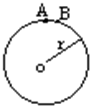 如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )
如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )
 如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )
如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )| A. | O处场强方向竖直向上 | |
| B. | O处场强方向竖直向下 | |
| C. | O处场强的大小为$\frac{klq}{{r}^{2}}$(k为静电力恒量,下同) | |
| D. | O处场强的大小为kq(2πr-l)r2 |
4.如图a所示,用一水平力F拉着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图b所示,根据图b中所提供的信息可以计算出( )
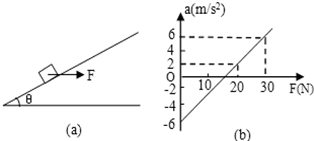

| A. | 物体的速度 | |
| B. | 斜面的倾角 | |
| C. | 物体能静止在斜面上所施加的最小外力 | |
| D. | 加速度为6 m/s2时物体的速度 |
5. 如图所示,某人身系弹性绳自高空P点自由下落,图中a点是弹性绳原长的位置,c点是人所到达的最低点,b点是人静止时悬吊的平衡位置,不计空气阻力,下列说法中正确的是( )
如图所示,某人身系弹性绳自高空P点自由下落,图中a点是弹性绳原长的位置,c点是人所到达的最低点,b点是人静止时悬吊的平衡位置,不计空气阻力,下列说法中正确的是( )
 如图所示,某人身系弹性绳自高空P点自由下落,图中a点是弹性绳原长的位置,c点是人所到达的最低点,b点是人静止时悬吊的平衡位置,不计空气阻力,下列说法中正确的是( )
如图所示,某人身系弹性绳自高空P点自由下落,图中a点是弹性绳原长的位置,c点是人所到达的最低点,b点是人静止时悬吊的平衡位置,不计空气阻力,下列说法中正确的是( )| A. | 从P至b过程中重力的冲量值大于弹性绳弹力的冲量值 | |
| B. | 从P至b过程中重力的冲量值与弹性绳弹力的冲量值相等 | |
| C. | 从P至c过程中重力的冲量值大于弹性绳弹力的冲量值 | |
| D. | 从P至c过程中重力的冲量值等于弹性绳弹力的冲量值 |
 一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可).
一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可).