题目内容
18. 一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可).
一士兵在训练,一根长l=5m的绳上端拴在O点,士兵抓住下端由静止摆下,运动到最低点时松手,而后落到地面上,O点右侧有一堵墙,墙与竖直方向的夹角为37°.为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过多少?(结果用三角函数表示即可).
分析 士兵先做圆周运动后做平抛运动,恰好要撞到墙上时速度与墙面相切,且有x=(y+l)tan37°,根据机械能守恒和平抛运动的规律求解.
解答 解:设士兵运动到最低点时的速度为v,则由机械能守恒得:
mgl(1-cosθ)=$\frac{1}{2}m{v}^{2}$
松手后他做平抛运动,水平位移为:x=vt
竖直位移为:y=$\frac{{v}_{y}^{2}}{2g}$
恰好撞到墙上时速度与墙面相切,则有:
vy=vtan37°=gt,t=$\frac{vtan37°}{g}$
且有:x=(y+l)tan37°.
代入得:$\frac{{v}^{2}tan37°}{g}$=($\frac{{v}^{2}ta{n}^{2}37°}{2g}$+l)tan37°
联立解得:cosθ=$\frac{7}{23}$,
即:θ=arccos$\frac{7}{23}$
答:为避免士兵撞到墙上,开始时,绳子与竖直方向的夹角θ不应超过arccos$\frac{7}{23}$.
点评 解决本题的关键是把握恰好撞到墙上时速度条件和位移条件,结合几何知识和运动学规律解答.

练习册系列答案
相关题目
9.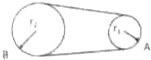 如图所示,A、B分别是两个轮子边缘上的点,两个轮子用皮带连起来且皮带不打滑,已知r1:r2=1:2,求A、B两点的向心加速度之比为( )
如图所示,A、B分别是两个轮子边缘上的点,两个轮子用皮带连起来且皮带不打滑,已知r1:r2=1:2,求A、B两点的向心加速度之比为( )
 如图所示,A、B分别是两个轮子边缘上的点,两个轮子用皮带连起来且皮带不打滑,已知r1:r2=1:2,求A、B两点的向心加速度之比为( )
如图所示,A、B分别是两个轮子边缘上的点,两个轮子用皮带连起来且皮带不打滑,已知r1:r2=1:2,求A、B两点的向心加速度之比为( )| A. | 1:2 | B. | 2:1 | C. | 1:1 | D. | 1:4 |
10.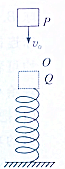 如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
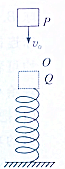 如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )| A. | 合力对物块做的功是-25J | B. | 物块的机械能守恒 | ||
| C. | 物块克服弹簧的弹力做的功是125J | D. | 物块的最大动能是110J |
16. 小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
 小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )| A. | 200N | B. | 100N | C. | 100$\sqrt{3}$N | D. | 200$\sqrt{2}$N |
 如图所示,在竖直平面内,粗糙的斜面轨道 AB 的下端与光滑的圆弧轨道BCD相切于B,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径 R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,D、E距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,r=10m/s2.求:
如图所示,在竖直平面内,粗糙的斜面轨道 AB 的下端与光滑的圆弧轨道BCD相切于B,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径 R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,D、E距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,r=10m/s2.求: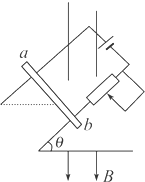 如图所示,在磁感应强度B=1.0T,方向竖直向下的匀强磁场中,有一个与水平面成θ=37°的导电滑轨,滑轨上放置一个可自由移动的金属杆ab,ab杆水平放置.已知接在滑轨中的电源电动势E=12V,内阻不计.导轨间距L=0.5m,质量m=0.2kg,杆与滑轨间的动摩擦因数μ=0.1,滑轨与ab杆的电阻忽略不计.求:要使ab杆在滑轨上保持静止,滑动变阻器R的阻值在什么范围内变化?(g取10m/s2,sin37°=0.6)
如图所示,在磁感应强度B=1.0T,方向竖直向下的匀强磁场中,有一个与水平面成θ=37°的导电滑轨,滑轨上放置一个可自由移动的金属杆ab,ab杆水平放置.已知接在滑轨中的电源电动势E=12V,内阻不计.导轨间距L=0.5m,质量m=0.2kg,杆与滑轨间的动摩擦因数μ=0.1,滑轨与ab杆的电阻忽略不计.求:要使ab杆在滑轨上保持静止,滑动变阻器R的阻值在什么范围内变化?(g取10m/s2,sin37°=0.6) 一质量为m,带电量为q(q>0)的粒子以速度v垂直进入宽度为L的有界匀强磁场中,如图所示,磁场方向垂直纸面向外,离开磁场的方向与边界成60°角,求匀强磁场的磁感应强度.(不计粒子的重力)
一质量为m,带电量为q(q>0)的粒子以速度v垂直进入宽度为L的有界匀强磁场中,如图所示,磁场方向垂直纸面向外,离开磁场的方向与边界成60°角,求匀强磁场的磁感应强度.(不计粒子的重力) 小球下落一段距离后,落在竖立的弹簧上,弹簧被压缩的过程中.
小球下落一段距离后,落在竖立的弹簧上,弹簧被压缩的过程中.