��Ŀ����
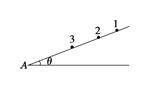
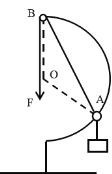
����Ŀ����ͼ��ʾΪ�ýʳ�������ʾ��ͼ��˩������ϸ�߱������������ϣ�������ʱ��ת���Ӷ��϶���顣��֪����İ뾶![]() ��ϸ��ʼ�ձ���ˮƽ�����϶��������ٶ�Ϊ�㣬����
��ϸ��ʼ�ձ���ˮƽ�����϶��������ٶ�Ϊ�㣬����![]() ��������Ķ�Ħ������
��������Ķ�Ħ������![]() ������Ľ��ٶ���ʱ��t�仯�Ĺ�ϵ��
������Ľ��ٶ���ʱ��t�仯�Ĺ�ϵ��![]() ��
��![]() ��gȡ
��gȡ![]() �������ж���ȷ����
�������ж���ȷ����![]() ����
����![]()

A. ���ļ��ٶ�������
B. ϸ�߶���������������
C. ǰ2�룬ϸ�߶�������Ĺ�Ϊ2J
D. ![]() ��ϸ�߶�����������˲ʱ����Ϊ12W
��ϸ�߶�����������˲ʱ����Ϊ12W
���𰸡�D
��������
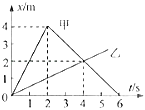
A��������֪�������ٶ�v=��R=2t��0.5=1t����v=at���ʿɵ�a=1m/s2�����������ȼ���ֱ���˶���ѡ��A����.
B����ţ�ٵڶ����ɿɵ�������ܺ�����F=ma=1N��F=T-f������Ħ������f=��mg=0.5��1��10=5N���ʿɵ����������������T=f+F=5+1=6N����B����.
C��������2s�ڵ�λ��![]() ������������Ϊ
������������Ϊ![]() ����C����.
����C����.
D��������2sĩ���ٶ�Ϊ![]() ����������˲ʱ����Ϊ
����������˲ʱ����Ϊ![]() ��D��ȷ.
��D��ȷ.
��ѡD.

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ