Question

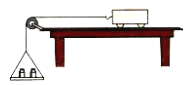
【题目】如图所示，小车内的地面是光滑的，左下角放一个小球B，右壁上挂一个相同的球A，两个球的质量均为4 kg，悬挂线与右壁成37°角，小车向右加速前进,此时右壁对A球的压力刚好为零（（g 取10 m/s2，sin37°=0.6，cos37°=0.8，tan37°=0.75）求：

⑴ 绳对A 球的拉力大小；

⑵ 左壁对B 球的压力大小；

⑶ 当小车的加速度 a=10 m/s2，时,绳对A球拉力大小

Answer 1

【答案】（1）50N（2）30N（3）56.5N

【解析】

（1）对小球A进行受力分析，根据牛顿第二定律求出绳对A球的拉力大小，并求得加速度。

（2）再对B球研究，结合牛顿第二定律列式求解左壁对B球的压力。

（3）小车向右加速运动的加速度a=10m/s2时小球A离开右壁，绳子拉力和重力的合力水平向右，由合成法求绳的拉力。

（1）设小车的加速度为a1，对小球A受力分析如下图所示。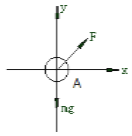

根据牛顿第二定律得：竖直方向有 Fcos37°=mg
可得绳子对A球的拉力大小 F=50N
（2）对A球，由牛顿第二定律得mgtan37°=ma1
解得：a1=gtan37°=7.5m/s2。
再以B球为研究对象，根据牛顿第二定律得
左壁对B球的压力大小N=ma1=4×7.5N=30N
（3）若小车向右加速运动的加速度a=10m/s2>a1=7.5m/s2，所以A球离开右壁，设绳与右壁的夹角是α．小球A的受力如下图所示。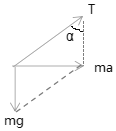

小球A的加速度水平向右，则合力水平向右，合力大小为ma，则