题目内容
2. 如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求:
如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求:(1)A、C两点的高度差;
(2)小物块刚要到达圆弧轨道末端D点时对轨道的压力;
(3)要使小物块不滑出长木板,木板的最小长度.
分析 (1)小球从A点抛出做平抛运动,将C点的速度进行分解,求出竖直分速度的大小,从而根据竖直方向上的运动规律求出AC两点的高度差.
(2)求出C点的速度,对C到D运用动能定理求出到达D点的速度,根据牛顿第二定律求出支持力的大小,从而得出物块对轨道的压力.
(3)当小物块刚好不从长木板滑出时,与木板具有相同的速度,根据牛顿第二定律和运动学公式求出共同的速度,结合位移公式进行求解.
解答 解:(1)小物块在C点时的速度大小为:
${v}_{c}=\frac{{v}_{0}}{cosθ}=\frac{1}{\frac{1}{2}}m/s=2m/s$,
竖直分量为:${v}_{cy}={v}_{c}sinθ=2×\frac{\sqrt{3}}{2}m/s=\sqrt{3}m/s$,
下落的高度为:h=$\frac{{{v}_{cy}}^{2}}{2g}=\frac{3}{20}m=0.15m$.
(2)小物块由C到D的过程中,由动能定理得:
$mgR(1-cosθ)=\frac{1}{2}m{{v}_{D}}^{2}-\frac{1}{2}m{{v}_{C}}^{2}$,
代入数据解得:vD=3m/s,
小球在D点时由牛顿第二定律得:${F}_{N}-mg=m\frac{{{v}_{D}}^{2}}{R}$,
代入数据解得:FN=28N,
由牛顿第三定律得,FN′=FN=28N,方向竖直向下.
(3)设小物块刚好滑到木板右端时与木板达到共同速度,大小为v,小物块在木板上滑行的过程中,小物块与长木板的加速度大小分别为:
${a}_{1}={μ}_{2}g=6m/{s}^{2}$,
${a}_{2}=\frac{{μ}_{2}mg-{μ}_{1}(m+M)g}{M}=9m/{s}^{2}$,
速度分别为v=vD-a1t=a2t,
代入数据解得t=$\frac{1}{5}s$,v=$\frac{9}{5}m/s$,
物块位移${x}_{1}=\frac{{v}_{D}+v}{2}t=\frac{3+\frac{9}{5}}{2}×\frac{1}{5}=\frac{12}{25}m$,
木板位移${x}_{2}=\frac{1}{2}{a}_{2}{t}^{2}=\frac{1}{2}×9×\frac{1}{25}m=\frac{9}{50}m$,
则L≥x1-x2=0.3m,即木板的长度至少是0.3m.
答:(1)A、C两点的高度差为0.15m;
(2)小物块刚要到达圆弧轨道末端D点时对轨道的压力为28N;
(3)要使小物块不滑出长木板,木板的最小长度为0.3m.
点评 本题综合考查了动能定理、牛顿第二定律、能量守恒定律等知识,综合性较强,关键理清物块的运动过程,选择合适的规律进行求解.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 质子 | B. | 中子 | C. | 电子 | D. | α粒子 |
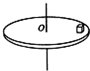 一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动,如图所示,那么下列说法正确的是( )
一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动,如图所示,那么下列说法正确的是( )| A. | 木块受到重力、支持力、摩擦力、向心力的作用 | |
| B. | 木块受到重力、支持力、摩擦力的作用 | |
| C. | 木块受到的摩擦力,方向始终是指向圆盘中心 | |
| D. | 木块受到的摩擦力,方向与木块的运动速度方向相反 |
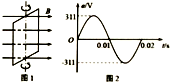 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示,产生的交变电动势的图象如图2所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示,产生的交变电动势的图象如图2所示,则( )| A. | t=0.015s时线框的电动势为零 | |
| B. | t=0.02s时线框平面与中性面垂直 | |
| C. | 线框产生的交变电动势有效值为311V | |
| D. | 该交变电动势瞬时值的表达式为e=311sin(100πt)V |
 一根轻质弹簧竖直悬挂在天花板上,下端悬挂一小球,小球和弹簧的受力如图所示,下列说法正确的是( )
一根轻质弹簧竖直悬挂在天花板上,下端悬挂一小球,小球和弹簧的受力如图所示,下列说法正确的是( )| A. | F1的施力者是弹簧 | B. | F2的反作用力是F3 | ||
| C. | 与F3平衡的力是F2 | D. | 与F4平衡的力是F1 |
| A. | 使两板带电量都加倍 | |
| B. | 使两板带电量都加倍,两板距离及正对面积都变为原来的4倍 | |
| C. | 使两板带电量都减半,两板距离变为原来的2倍 | |
| D. | 使两板距离加倍,两板正对面积变为原来的4倍 |
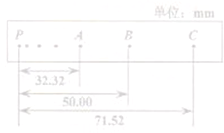 在“验证机械能守恒定律”的一次实验中,质量为1kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点的时间间隔为0.02s,当地的重力加速度g=9.8m/s2,回答以下问题,计算结果均保留两位有效数字.
在“验证机械能守恒定律”的一次实验中,质量为1kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点的时间间隔为0.02s,当地的重力加速度g=9.8m/s2,回答以下问题,计算结果均保留两位有效数字.
 如图所示,把质量为0.5kg的石块从30m高处的A点以300角斜向上方抛出,初速度是v0=5m/s(不计空气阻力,取g=10m/s2)求:
如图所示,把质量为0.5kg的石块从30m高处的A点以300角斜向上方抛出,初速度是v0=5m/s(不计空气阻力,取g=10m/s2)求: