题目内容
10.如图甲所示,一对足够长平行、粗糙、电阻不计的导轨固定在水平面上,导轨间距l=1m,左端之间用R=3Ω的电阻连接.一根质量m=0.5kg、电阻r=1Ω、长度也为1m的导体杆垂直导轨静置在两导轨上,整个装置处于竖直向上,磁感应强度B=2T的匀强磁场中.现用水平向右的拉力F拉导体杆、拉力F与时间t的关系如图乙所示,导体杆恰好做匀加速直线运动,在0~2s内拉力F所做的功为W=$\frac{68}{3}$J,重力加速度g取10m/s2.求:
(1)导体杆与导轨间的动摩擦因数μ;
(2)在0~2s内通过电阻R的电量q;
(3)在0~2s内电阻R上产生的热量Q.
分析 (1)根据切割产生的感应电动势公式、闭合电路欧姆定律和安培力公式求出导体杆所受安培力与时间的关系式,结合牛顿第二定律求出拉力D与t的关系式,根据F-t图线求出匀加速直线运动的加速度和动摩擦因数.
(2)根据匀变速直线运动的位移时间公式求出导体杆的位移,通过q=$\frac{△Φ}{R+r}$求出通过电阻R的电量.
(3)求出2s末导体杆的速度,抓住克服安培力做功等于整个回路产生的热量,根据动能定理求出整个回路产生的热量,从而求出电阻R上产生的热量.
解答 解:(1)设导体杆的加速度为a,则t时刻导体杆的速度 v=at
产生的感应电动势为 E=Blv
电路中的感应电流为 I=$\frac{Blv}{R+r}$
导体杆上所受的安培力为 F安=BIl=$\frac{{B}^{2}{l}^{2}v}{R+r}$=$\frac{{B}^{2}{l}^{2}at}{R+r}$
由牛顿第二定律可知 F-μmg-$\frac{{B}^{2}{l}^{2}at}{R+r}$=ma
即F=ma+μmg+$\frac{{B}^{2}{l}^{2}at}{R+r}$
代入数字得 F=($\frac{1}{2}$a+5μ+at)N
由图象可知 F=3+2t N
由于物体做匀加速直线运动,加速度a为常数,比较两式可得
a=2 m/s2,μ=0.4
(2)在F作用的时间内,导体杆的位移为 x=$\frac{1}{2}$at2=4 m
在时间t内的平均感应电动势 $\overline{E}$=$\frac{△Φ}{△t}$=$\frac{Blx}{t}$
平均电流为 $\overline{I}$=$\frac{Blx}{t(R+r)}$
通过的电荷量 q=$\overline{I}$t=$\frac{Blx}{R+r}$
代入数得q=2 C
(3)t=2s时刻,导体杆的速度v=at=4 m/s
在力F的作用过程中,设电路中产生的总热量为Q′.由动能定理可知
WF-μmgx-Q′=$\frac{1}{2}$mv2
代入数字可得 Q′=$\frac{32}{3}$J
由串联电路的知识可知 Q=$\frac{3}{4}$Q′=8 J
答:(1)导体杆与导轨间的动摩擦因数为0.4.(2)在0~2s内通过电阻R的电量为2C.(3)在0~2s内电阻R上产生的热量为8J.
点评 考查根据图象寻找有价值的信息,并结合法拉第电磁感应定律、牛顿第二定律、闭合电路欧姆定律、能量守恒定律综合求解.注意巧用小方格来得出这段时间内的位移

| A. | 式中k值,对所有行星和卫星都相等 | |
| B. | 围绕不同恒星运行的行星,其k值一般不同 | |
| C. | 公式只适用于绕太阳做椭圆轨道运行的行星 | |
| D. | 公式适用于宇宙中所有围绕恒星运动的行星 |
 如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )
如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )| A. | Wa=Wb | B. | Wa<Wb | ||
| C. | Wa>Wb | D. | 以上三种情况都有可能 |
| A. | 该星球的密度是地球密度的2倍 | |
| B. | 该星球表面的重力加速度是地球表面重力加速度的4倍 | |
| C. | 该星球的近地卫星的速度是地球近地卫速度的4倍 | |
| D. | 该星球的近地卫星周期跟地球的近地卫星周期相等 |
| A. | 研究胡克定律 | |
| B. | 研究瞬时速度 | |
| C. | 利用速度-时间图象研究匀变速直线运动的位移 | |
| D. | 研究加速度与力、质量的关系 |
| A. | 空调既能制热又能制冷,说明热传递不存在方向性 | |
| B. | 只有在体积一定时,饱和汽压才随温度的升高而增大 | |
| C. | 分子间作用力的合力表现为引力时,若分子间的距离增大,则分子力不一定减小,但分子势能一定增大 | |
| D. | 沸点与大气压有关,大气压较高时沸点比较低 |
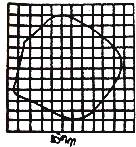 在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题:
在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题: 如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求:
如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求: