题目内容
13.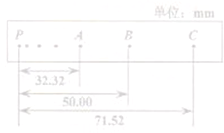 在“验证机械能守恒定律”的一次实验中,质量为1kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点的时间间隔为0.02s,当地的重力加速度g=9.8m/s2,回答以下问题,计算结果均保留两位有效数字.
在“验证机械能守恒定律”的一次实验中,质量为1kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点的时间间隔为0.02s,当地的重力加速度g=9.8m/s2,回答以下问题,计算结果均保留两位有效数字.(1)纸带的左(选填“左”或“右”)端与重物相连;
(2)打点计时器应接交流(选填“直流”或“交流”)电流,实验时应先接通电源(填“释放纸带”或“接通电源”);
(3)从起点P到打下计数点B的过程中物体的重力势能减少量△EP=0.49J,此过程中物体动能的增加量△Ek=0.48J;
(4)在上述验证机械能守恒定律的实验中发现,重锤减小的重力势能大于重锤动能的增加,若其原因是由于在重锤下落的过程中存在阻力作用,通过以上实验数据可以测出重锤在下落过程中受到的平均阻力大小F=0.20N.
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.应用打点计时器时,要先接通电源,然后再放开纸带.根据牛顿第二定律求出阻力的大小.
解答 解:(1)从纸带上可以看出P点为先打出来的点,重物自由下落,而与重物相连的纸带在下端,应该先打点.所以纸带的左端应与重物相连.
(2)打点计时器应接交流电源,应用打点计时器时,要先接通电源,然后再放开纸带,
如果先释放纸带后接通电源,有可能会出现小车已经拖动纸带运动一段距离,电源才被接通,那么纸带上只有很小的一段能打上点,大部分纸带没有打上点,纸带的利用率太低.所以应当先接通电源,待打点稳定后再用手牵动纸带.
(3)重力势能减小量为:△Ep=mgh=1×9.8×0.050J=0.49J.
利用匀变速直线运动的推论:
vB=$\frac{0.07152-0.03232}{2×0.02}$=0.98m/s
动能增加量为:△Ek=$\frac{1}{2}$mvB2=0.48J.
(4)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,得:
xBC-xAB=aT2
a=$\frac{(0.07152-0.050)-(0.050-0.03232)}{0.0{2}^{2}}$=9.6m/s2
根据牛顿第二定律得:mg-F=ma
受到的平均阻力大小为:F=mg-ma=1×9.8-1×9.6=0.20N
故答案为:(1)左;(2)交流,接通电源;(3)0.49,0.48;(4)0.20.
点评 纸带问题的处理是力学实验中常见的问题.在纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,计算过程中要注意单位的换算.

| A. | 亚里士多德首先建立了平均速度、瞬时速度、加速度等描述运动所需的概念 | |
| B. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| C. | 在对自由落体运动的研究中,伽利略猜想运动速度与下落时间成正比,并直接用实验进行了验证 | |
| D. | 落体下落很快,不容易计时,伽利略让小球沿阻力很小的斜面滚下,用“冲淡”重力的巧妙方法加以突破 |

| A. | 物块在4s内位移是6m | B. | 物块的质量是2kg | ||
| C. | 物块与水平面间动摩擦因数是0.4 | D. | 物块在4s内电势能减少了14J |
| A. | 式中k值,对所有行星和卫星都相等 | |
| B. | 围绕不同恒星运行的行星,其k值一般不同 | |
| C. | 公式只适用于绕太阳做椭圆轨道运行的行星 | |
| D. | 公式适用于宇宙中所有围绕恒星运动的行星 |
| A. | 电场线是电荷移动的轨迹 | |
| B. | 电场线是实际存在的曲线 | |
| C. | 电场线是闭合的曲线 | |
| D. | 电场线是起始于正电荷(或无穷远),终止于负电荷(或无穷远)的不闭合曲线 |
 如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )
如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )| A. | Wa=Wb | B. | Wa<Wb | ||
| C. | Wa>Wb | D. | 以上三种情况都有可能 |
 如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求:
如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=0.5kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间的动摩擦因数μ1=0.1,小物块与长木板间的动摩擦因数μ2=0.6,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,取重力加速度g=10m/s2.求: 如图所示,轻杆长为3L,在轻杆的两端分别固定了质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,当球B运动到最高点时,球B对杆恰好无作用力.已知重力加速度为g.求:
如图所示,轻杆长为3L,在轻杆的两端分别固定了质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,当球B运动到最高点时,球B对杆恰好无作用力.已知重力加速度为g.求: