题目内容
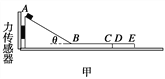
【题目】如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.求: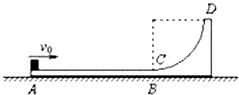
(1)小物块与水平轨道的动摩擦因数μ.
(2)为了保证小物块不从轨道的D端离开轨道,圆弧轨道的半径R至少是多大?
(3)若圆弧轨道的半径R取第(2)问计算出的最小值,增大小物块的初动能,使得小物块冲上轨道后可以达到最大高度是1.5R处,试求物块的初动能并分析物块能否停在水平轨道上.如果能,将停在何处?如果不能,将以多大速度离开水平轨道.
【答案】
(1)解:小物块最终停在AB的中点,在这个过程中,由动能定理得:﹣μmg(L+0.5L)=﹣E
得:μ= ![]()
答:小物块与水平轨道的动摩擦因数μ为 ![]() .
.
(2)解:若小物块刚好到达D处,速度为零,同理,有:﹣μmgL﹣mgR=﹣E
解得CD圆弧半径至少为:R= ![]()
答:为了保证小物块不从轨道的D端离开轨道,圆弧轨道的半径R至少是 ![]() .
.
(3)解:设物块以初动能E′冲上轨道,可以达到的最大高度是1.5R,由动能定理得:
﹣μmgL﹣1.5mgR=﹣E′
解得:E′= ![]()
物块滑回C点时的动能为EC=1.5mgR= ![]() ,由于EC<μmgL=
,由于EC<μmgL= ![]() ,故物块将停在轨道上.
,故物块将停在轨道上.
设到A点的距离为x,有﹣μmg(L﹣x)=﹣EC
解得:x= ![]() L
L
即物块最终停在水平滑道AB上,距A点 ![]() L处.
L处.
答:物块最终停在水平滑道AB上,距A点 ![]() L处.
L处.
【解析】(1)在小物块运动的整个过程中,重力做功为0,摩擦力做负功﹣1.5μmgL,根据动能定理求解μ.(2)小物块恰好不从轨道的D端离开轨道时,到达D点速度为零,由动能定理求出R.(3)根据动能定理求解出小物块恰好冲上最大高度1.5R时的初动能E′,物块滑回C点时的动能EC=1.5mgR,分析EC与滑块从B到A克服摩擦力做功的大小关系,即可判断物块能否停在水平轨道上.并能根据动能定理求解滑块停止在轨道何处.
【考点精析】根据题目的已知条件,利用动能定理的综合应用的相关知识可以得到问题的答案,需要掌握应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案