Question

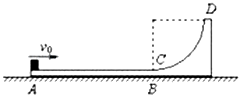
【题目】如图甲所示，由斜面AB和水平面BC组成的物块，放在光滑水平地面上，斜面AB部分光滑，AB长度为s＝2.5 m，水平部分BC粗糙．物块左侧与竖直墙壁之间连接着一个力传感器，当传感器受压时示数为正值，被拉时为负值．上表面与BC等高且粗糙程度相同的木板DE紧靠在物块的右端，木板DE质量M＝4 kg，长度L＝1.5 m．一可视为质点的滑块从A点由静止开始下滑，经B点由斜面转到水平面时速度大小不变．滑块从A到C过程中，传感器记录到力和时间的关系如图乙所示．g取10 m/s2，求：

　

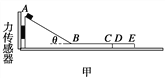
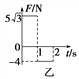
(1)斜面AB的倾角θ；

(2)滑块的质量m；

(3)滑块到达木板DE右端时的速度大小．

Answer 1

【答案】(1)30°　(2)2 kg　(3)1 m/s

【解析】试题分析：（1）在0～1 s内木块沿斜面匀加速下滑：mgsin θ＝ma ①

s＝at2 ②

由图知：t＝1 s

解得：sin θ＝，故θ＝30°. ③

（2）在0～1 s内对斜面体ABC受力分析：mgcos θ sin θ－F＝0 ④

由图知：F＝5N

解得：m＝2 kg. ⑤

（3）木块到达B点的速度：vB＝at＝gsin θt＝5 m/s ⑥

1～2 s木块在BC部分做减速运动：μmg＝ma′⑦

对斜面体，由图象知：μmg＝F＝4 N⑧

解得：a′＝2 m/s2，μ＝0.2

木块到达C点时：vC＝vB－a′t＝vB－μgt＝3 m/s⑨

木块滑上木板DE时：对木块：－μmg＝ma1⑩

对木板：μmg＝Ma2

解得：a1＝－2 m/s2，a2＝1 m/s2

设木块在木板上的滑行时间为t，

x木块＝vCt＋a1t2

x木板＝a2t2

L＝x木块－x木板

解得：t＝1s

此时，木块速度：v木块＝vC－a1t＝1 m/s

木板速度：v木板＝a2t＝1 m/s

所以木块恰好滑到木板右端，速度为1 m/s.