题目内容
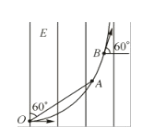
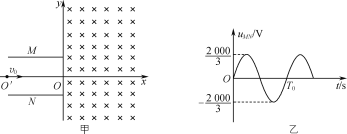
【题目】如图甲所示,平行金属板M、N水平放置,板长L=![]() m、板间距离d=0.20m。在竖直平面内建立xOy直角坐标系,使x轴与金属板M、N的中线OO′重合,y轴紧靠两金属板右端。在y轴右侧空间存在方向垂直纸面向里、磁感应强度大小B=5.0×10-3T的匀强磁场,M、N板间加随时间t按正弦规律变化的电压uMN,如图乙所示,图中T0未知,两板间电场可看作匀强电场,板外电场可忽略。比荷
m、板间距离d=0.20m。在竖直平面内建立xOy直角坐标系,使x轴与金属板M、N的中线OO′重合,y轴紧靠两金属板右端。在y轴右侧空间存在方向垂直纸面向里、磁感应强度大小B=5.0×10-3T的匀强磁场,M、N板间加随时间t按正弦规律变化的电压uMN,如图乙所示,图中T0未知,两板间电场可看作匀强电场,板外电场可忽略。比荷![]() =1.0×107C/kg、带正电的大量粒子以v0=1.0×105m/s的水平速度,从金属板左端沿中线OO′连续射入电场,进入磁场的带电粒子从y轴上的 P、Q(图中未画岀,P为最高点、Q 为最低点)间离开磁场。在每个粒子通过电场区域的极短时间内,电场可视作恒定不变,忽略粒子重力,求:
=1.0×107C/kg、带正电的大量粒子以v0=1.0×105m/s的水平速度,从金属板左端沿中线OO′连续射入电场,进入磁场的带电粒子从y轴上的 P、Q(图中未画岀,P为最高点、Q 为最低点)间离开磁场。在每个粒子通过电场区域的极短时间内,电场可视作恒定不变,忽略粒子重力,求:
(1) 进入磁场的带电粒子在电场中运动的时间t0及在磁场中做圆周运动的最小半径r0;
(2) P、Q两点的纵坐标yP、yQ;
(3) 若粒子到达Q点的同时有粒子到达P点,满足此条件的电压变化周期T0的最大值。
【答案】(1)3.46×10-6 s;2.0 m;(2) 4.1 m;3.9 m;(3) 2.51×10-4 s
【解析】
(1) 能从右侧离开电场的带电粒子在电场中运动的时间
t0=![]()
代入数据得t0=3.46×10-6 s
t=![]() nT0(n=0、1、2……)时刻射入电场的带电粒子不发生偏转,进入磁场做圆周运动的半径最小。粒子在磁场中运动时有
nT0(n=0、1、2……)时刻射入电场的带电粒子不发生偏转,进入磁场做圆周运动的半径最小。粒子在磁场中运动时有
qv0B=![]()
代入数据解得r0=2.0 m
(2) 设两板间电压为U1时,带电粒子刚好从极板边缘射出电场,则有
q![]() =ma,
=ma,![]() d=
d=![]() at
at
代入数据解得U1=![]() V
V
在电压小于等于![]() V时,带电粒子才能从两板间射出电场,电压大于
V时,带电粒子才能从两板间射出电场,电压大于![]() V时,带电粒子打在极板上,不能从两板间射出。带电粒子刚好从极板边缘射出电场时,速度最大。
V时,带电粒子打在极板上,不能从两板间射出。带电粒子刚好从极板边缘射出电场时,速度最大。
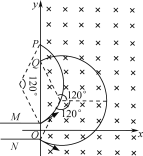
设粒子恰好射出电场时速度为v,方向与x轴的夹角为θ,在磁场中做圆周运动的半径为r,则
tan θ=![]() ,qvB=
,qvB=![]()
弦长
D=2rcos θ
代入数据解得
θ=30°
则有
D=![]() =4.0 m
=4.0 m
从极板M边缘射出的带电粒子,在磁场中转过120°,经过P点,则
yP=![]() +D=4.1 m
+D=4.1 m
从极板N边缘射出的带电粒子,在磁场中转过240°,经过Q点,则
yQ=D-![]() =3.9 m
=3.9 m
(3)带电粒子在磁场中做圆周运动的周期T=![]() ,粒子到达Q点的同时有粒子到达P点,则这两个粒子开始运动的时间差为
,粒子到达Q点的同时有粒子到达P点,则这两个粒子开始运动的时间差为![]() ,到达Q点的粒子进入磁场的时刻可能是
,到达Q点的粒子进入磁场的时刻可能是![]() 、
、![]() 、
、![]() 、
、![]() ……到达P点的粒子进入磁场的时刻可能是
……到达P点的粒子进入磁场的时刻可能是![]() 、
、![]() 、
、![]() 、
、![]() ……,当电压变化周期T0有最大值Tm时应满足的关系
……,当电压变化周期T0有最大值Tm时应满足的关系
![]() -
-![]()
![]()
解得
Tm=![]() ×10-4 s=2.51×10-4 s
×10-4 s=2.51×10-4 s