题目内容
 (2012?新余模拟)如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为u,划船速度均为v,出发时两船相距
(2012?新余模拟)如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为u,划船速度均为v,出发时两船相距| 2 |
| 3 |
| 3 |
分析:小船过河的速度为船本身的速度垂直河岸方向的分速度,故要求过河时间需要将船速分解为沿河岸的速度和垂直河岸的速度;要求两船相遇的地点,需要求出两船之间的相对速度,即它们各自沿河岸的速度的和;由于知道了它们过河的时间,故可以求出甲船靠岸的地点.
解答:解:小船过河的速度为船本身的速度垂直河岸方向的分速度,故小船过河的速度vy=vsin60°,故小船过河的时间:
t1=
=
,故甲乙两船到达对岸的时间相同,故A正确;
甲船沿河岸方向的速度:v1+u=vcos60°+u=u+
乙船沿河岸方向的速度:v2-u=vcos60°-u=
-u
故甲乙两船沿河岸方向的相对速度为:u+
+
-u=v
故两船相遇的时间为:t2=
H÷v=
=t1,
故两船在到达对岸时相遇,故B错误;
由于乙船恰好能直达对岸的A点,而两船在到达对岸时相遇,故甲船在A点到达对岸,故C错误,而D正确;
故选AD.
t1=
| H |
| Vy |
2
| ||
| 3v |
甲船沿河岸方向的速度:v1+u=vcos60°+u=u+
| v |
| 2 |
乙船沿河岸方向的速度:v2-u=vcos60°-u=
| v |
| 2 |
故甲乙两船沿河岸方向的相对速度为:u+
| v |
| 2 |
| v |
| 2 |
故两船相遇的时间为:t2=
| 2 |
| 3 |
| 3 |
2
| ||
| 3v |
故两船在到达对岸时相遇,故B错误;
由于乙船恰好能直达对岸的A点,而两船在到达对岸时相遇,故甲船在A点到达对岸,故C错误,而D正确;
故选AD.
点评:本题考查了运动的合成与分解,相对速度,小船过河问题,注意过河时间由垂直河岸的速度与河宽决定.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 (2012?新余模拟)完全相同的直角三角形滑块A、B,按如图2-3-27所示叠放,设A、B接触的斜面光滑,A与桌面间的动摩擦因数为μ,现在B上作用一水平推力F,恰好使A、B一起在桌面上匀速运动,且A、B保持相对静止.则A与桌面间的动摩擦因数μ与斜面倾角θ的关系为( )
(2012?新余模拟)完全相同的直角三角形滑块A、B,按如图2-3-27所示叠放,设A、B接触的斜面光滑,A与桌面间的动摩擦因数为μ,现在B上作用一水平推力F,恰好使A、B一起在桌面上匀速运动,且A、B保持相对静止.则A与桌面间的动摩擦因数μ与斜面倾角θ的关系为( )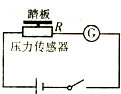 (2012?新余模拟)有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(是一个阻值可随压力大小而变化的电阻器)、显示体重的仪表G(实质是理想电流表),设踏板的质量可忽略不计,已知理想电流表的量程为3A,电源电动势为12V,内阻为2Ω,电阻R随压力变化的函数式为R=
(2012?新余模拟)有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(是一个阻值可随压力大小而变化的电阻器)、显示体重的仪表G(实质是理想电流表),设踏板的质量可忽略不计,已知理想电流表的量程为3A,电源电动势为12V,内阻为2Ω,电阻R随压力变化的函数式为R= (2012?新余模拟)质量M=0.6kg的平板小车静止在光滑水面上,如图所示,当t=0时,两个质量都为m=0.2kg的小物体A和B,分别从小车的左端和右端以水平速度v1=5.0m/s和v2=2.0m/s同时冲上小车,当它们相对于小车停止滑动时,没有相碰.已知A、B两物体与车面的动摩擦因数都是0.20,取g=10m/s2,求:
(2012?新余模拟)质量M=0.6kg的平板小车静止在光滑水面上,如图所示,当t=0时,两个质量都为m=0.2kg的小物体A和B,分别从小车的左端和右端以水平速度v1=5.0m/s和v2=2.0m/s同时冲上小车,当它们相对于小车停止滑动时,没有相碰.已知A、B两物体与车面的动摩擦因数都是0.20,取g=10m/s2,求: