Question

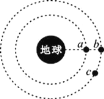
【题目】如图所示，三颗卫星a、b、c均绕地球做匀速圆周运动，其中b、c在地球的同步轨道上，a距离地球表面的高度为R，此时a、b恰好相距最近。已知地球质量为M、半径为R、地球自转的角速度为。万有引力常量为G，则（ ）

A.发射卫星b、c时速度要大于

B.b、c卫星离地球表面的高度为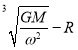

C.卫星a和b下一次相距最近还需经过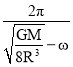

D.若要卫星c与b实现对接，可让卫星b减速

Answer 1

【答案】BC

【解析】

A．卫星b、c绕地球做匀速圆周运动，7.9km/s是指在地球上发射的物体绕地球飞行作圆周运动所需的最小初始速度，11.2km/s是物体挣脱地球引力束缚的最小发射速度。所以发射卫星b时速度大于7.9km/s，而小于11.2km/s，故A错误；
B．万有引力提供向心力，对b、c卫星，由牛顿第二定律得

解得

故B正确；
C．卫星b在地球的同步轨道上，所以卫星b和地球具有相同的周期和角速度。由万有引力提供向心力，即

解得

a距离地球表面的高度为R，所以卫星a的角速度

此时a、b恰好相距最近，到卫星a和b下一次相距最近

（ωa-ω）t=2π

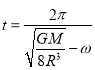
故C正确；
D．让卫星b减速，卫星b所需的向心力减小，万有引力大于所需的向心力，卫星b会做向心运动，轨道半径变小，离开原轨道，所以不能与c对接，故D错误；

故选BC。