题目内容
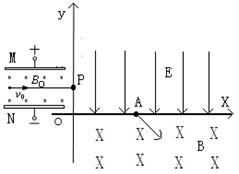
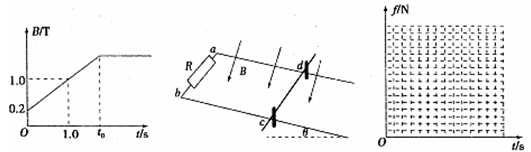
(22分)如图甲所示,水平放置的A、B两平行金属板的中央各有一小孔O1、O2,板间距离为d,开关S接1。当t=0时,在a、b两端加上如图乙中的①图线所示的电压,同时在c、d两端加上如图丙所示的电压。此时,一质量为m的带负电微粒恰好静止于两孔连线的中点P处 (P、O1、O2在同一竖直线上)。重力加速度为g,空气阻力和金属板的厚度不计。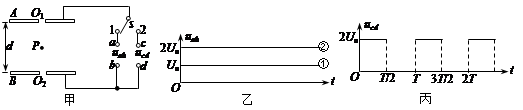
⑴若某时刻突然在a、b两端改加如图乙中的②图线所示的电压,则微粒可达到的最高点距A板的高度为多少?
⑵试在答题卷所给的坐标中,定性画出在a、b两端改加如图乙中的②图线所示的电压之后微粒运动过程中相对于P点的重力势能Ep随时间t变化的图象(只要求画出图线,不必写出定量关系式,但必须标明各转折点的横纵坐标);
⑶若要使微粒在两板间运动一段时间后,从A板中的O1小孔射出,且射出时的动能尽可能大,问应在t=0到t=T之间的哪个时 刻把开关s从l扳到2位置?ucd的变化周期T至少为多少?
(1)h=d/2 (2)见解析 (3)在 时刻把开关s从1扳到2
时刻把开关s从1扳到2 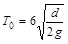
解析试题分析:⑴微粒P可达到的最高点距A板的高度为h,则有: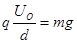 (2分)
(2分)  (2分)
(2分)
解得: h="d/2" (1分)
⑵ 如图所示 (4分)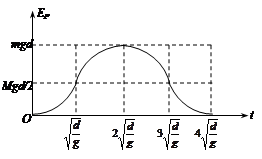
⑶当A、B间电压为2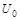 时,根据牛顿第二定律,有
时,根据牛顿第二定律,有 (2分)
(2分)
得a=g(1分)
依题意,为使微粒P以最大的动能从小孔 射出,应让微粒P能从
射出,应让微粒P能从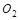 处无初速向上一直做匀加速运动。为此,微粒P应先自由下落一段时间,然后加上电压2
处无初速向上一直做匀加速运动。为此,微粒P应先自由下落一段时间,然后加上电压2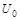 ,使微粒P接着以大小为g的加速度向下减速到
,使微粒P接着以大小为g的加速度向下减速到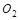 处再向上加速到
处再向上加速到 孔射出。设向下加速和向下减速的时间分别为t1和t2,则
孔射出。设向下加速和向下减速的时间分别为t1和t2,则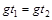 (2分)
(2分) (2分)
(2分)
解得: 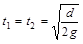 (1分)
(1分)
故应在 时刻把开关s从1扳到2(1分)
时刻把开关s从1扳到2(1分)
设电压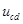 的最小周期为T0,向上加速过程,有:
的最小周期为T0,向上加速过程,有: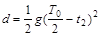 (3分)
(3分)
解得: 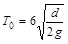 (1分)
(1分)
考点: 静电场、共点力平衡、牛顿第二定律、交变电流

 阅读快车系列答案
阅读快车系列答案如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30 的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )
的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )
| A.甲球机械能不守恒,乙球机械能守恒 |
B.甲、乙两球的质量之比为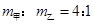 |
C.甲、乙两球的动能均为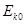 时,两球重力的瞬时功率之比为 时,两球重力的瞬时功率之比为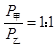 |
D.甲、乙两球的动能均为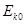 时,两球高度相同 时,两球高度相同 |

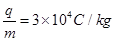 的带电粒子经一电场U=150V加速进入到一只有左边界的匀强磁场中,已知匀强磁场的磁感应强度为B="0.1T" 求:
的带电粒子经一电场U=150V加速进入到一只有左边界的匀强磁场中,已知匀强磁场的磁感应强度为B="0.1T" 求: