题目内容
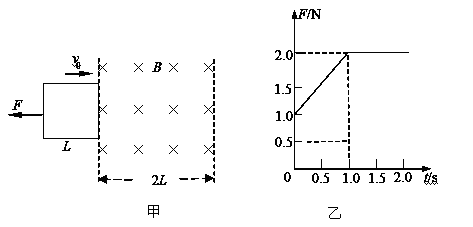
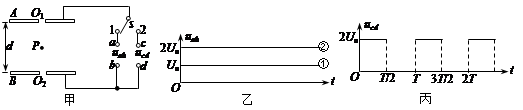
两根平行金属导轨固定倾斜放置,与水平面夹角为37°,相距d="0.5" m,a、b间接一个电阻R,R="1.5" Ω.在导轨上c、d两点处放一根质量m=0.05 kg的金属棒,bc长L="1" m,金属棒与导轨间的动摩擦因数μ=0.5.金属棒在导轨间的电阻r="0.5" Ω,金属棒被两个垂直于导轨的木桩顶住而不会下滑,如图所示.在金属导轨区域加一个垂直导轨斜向下的匀强磁场,磁场随时间的变化关系如图所示,重力加速度g=" 10" m/s2.可认为最大静摩擦力与滑动摩擦力相等,(sin37°=0.6,cos 37° =0.8).求: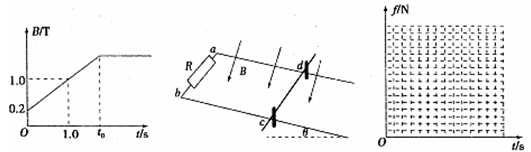
(1)0~1.0 s内回路中产生的感应电动势大小;
(2)t=0时刻,金属棒所受的安培力大小;
(3)在磁场变化的全过程中,若金属棒始终没有离开木桩而上滑,则图4中t0的最大值;
(4)通过计算在图6中画出0~t0max内金属棒受到的静摩擦力随时间的变化图象.
(1)0.4 V (2) 0.02 N (3)6 s (4) 如下图所示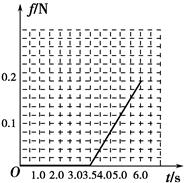
解析试题分析:(1)读题图可知: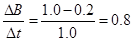 T/s,
T/s,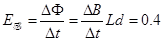 V。
V。
(2)感应电流: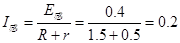 A
A
安培力:F安0=B0I感d=0.2×0.2×0.5 N=0.02 N。
(3)金属棒对木桩的压力为零,最大静摩擦力沿斜面向下,此时沿倾斜导轨方向上合外力为零. 若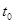 时刻棒恰未上滑,则
时刻棒恰未上滑,则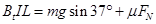
又由图知: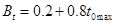
联立可得: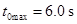 即为所求。
即为所求。
一开始,木桩对金属棒有支持力,金属棒对导轨无相对运动趋势,静摩擦力f静=0。随着安培力F安的增大,木桩对金属棒的弹力减小,直至弹力为零,满足:F安=B(t)I感d=mgsin 37°
代入数据:(0.2+0.8t)×0.2×0.5=0.05×10×0.6,得:t=3.5 s
F安继续增大,f静从零开始增大
F安=B(t)I感d=(0.2+0.8t)×0.2×0.5=mgsin 37°+f静
所以f随t线性增大至f=0.2 N(此时t0max=6 s).
考点:本题考查电磁感应的图象、法拉第电磁感应定律、闭合电路的欧姆定律、力的平衡条件和摩擦力等综合知识。

一个小球做自由落体运动,在第1s内重力做功为W1,在第2s内重力做功为W2;在第1s末重力的瞬时功率为P1,在第2s末重力的瞬时功率做功为P2,则W1:W2及P1:P2分别等于( )
| A.1:1,1:1 | B.1:2,1:3 | C.1:3;1:2 | D.1:4,1:2 |
一人乘电梯从1楼到20楼,在此过程中经历了先加速,后匀速,再减速的运动过程,则电梯支持力对人做功情况是
| A.加速时做正功,匀速时不做功,减速时做负功 |
| B.加速时做正功,匀速和减速时做负功 |
| C.加速和匀速时做正功,减速时做负功 |
| D.始终做正功 |
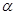 =45°。求:
=45°。求: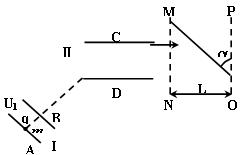

 坐标系坐标原点O处有一点状的放射源,它向
坐标系坐标原点O处有一点状的放射源,它向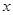 轴上方各个方向发射
轴上方各个方向发射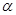 粒子,
粒子,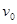 ,在
,在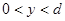 的区域内分布有指向
的区域内分布有指向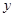 轴正方向的匀强电场,场强大小为
轴正方向的匀强电场,场强大小为 ,其中
,其中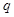 与
与 分别为
分别为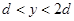 的区域内分布有垂直于
的区域内分布有垂直于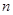 为电场和磁场的边界.
为电场和磁场的边界.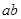 为一块很大的平面感光板垂直于
为一块很大的平面感光板垂直于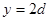 处,如图所示.观察发现此时恰好无粒子打到
处,如图所示.观察发现此时恰好无粒子打到
 的大小;
的大小;