题目内容
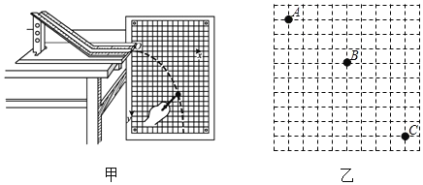
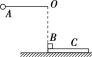
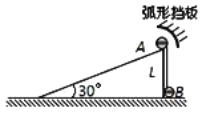
【题目】如图所示,倾角30°高为L的固定斜面底端与水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端。现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上。已知重力加速度为g,不计一切摩擦,则( )
A.小球A下滑过程中,小球A、B系统的重力势能减小
B.A球刚滑至水平面时的速度大小为![]()
C.小球B升高![]() 时,重力对小球A做功的功率大于重力对小球B做功的功率
时,重力对小球A做功的功率大于重力对小球B做功的功率
D.小球B从刚开始上升到开始进入斜面过程中,绳的拉力对小球B做功为![]()
【答案】ABC
【解析】
A.小球A下滑过程中,小球A、B组成的系统机械能守恒,由于A沿斜面的下滑分力大于小球B的重力,因此B在上升过程中,整个系统做加速运动,动能增加,因此整个系统,重力势能一定减小,A正确;
B.根据机械能守恒定律
![]()
整理得
![]()
B正确;
C.设小球B升高![]() 时,小球A、B的速度大小为
时,小球A、B的速度大小为![]()
则重力对A做功的功率为
![]()
重力对B做功的功率大小为
![]()
可知
![]()
C正确;
D.在B上升的过程中,对小球A进行受力分析,根据牛顿第二定律,可得
![]()
对B进行受力分析,根据牛顿第二定律
![]()
两式联立得,绳子拉力
![]()
小球B从刚开始上升到开始进入斜面过程中,绳的拉力对小球B做功为
![]()
D错误。
故选ABC。

练习册系列答案
相关题目