题目内容
【题目】如图所示，用长为R的不可伸长的轻绳将质量为
的小球A悬挂于O点．在光滑的水平地面上，质量为m的小物块B（可视为质点）置于长木板C的左端静止．将小球A拉起，使轻绳水平拉直，将A球由静止释放，运动到最低点时与小物块B发生弹性正碰．
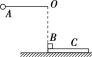
（1）求碰后轻绳与竖直方向的最大夹角θ的余弦值．
（2）若长木板C的质量为2m，小物块B与长木板C之间的动摩擦因数为μ，长木板C的长度至少为多大，小物块B才不会从长木板C的上表面滑出？
【答案】（1）
（2）
【解析】
（1）设小球A与小物块B碰前瞬间的速度为v0，则有
设碰后小球A和小物块B的速度分别为v1和v2，有
v0＝v1＋mv2
设碰后小球A能上升的最大高度为H，有
所求
cos θ＝
由以上各式解得
cos θ＝
.
（2）法一：由（1）可求得碰后小物块B的速度为
v2＝
设小物块B与长木板C相互作用达到的共同速度为v，长木板C的最小长度为L，有
mv2＝（m＋2m）v
μmgL＝
mv22－（m＋2m）v2
由以上各式解得
L＝
.
法二：由（1）可求得碰后小物块B的速度为
v2＝
设小物块B运动位移为x1时，小物块B、长木板C达到共同速度v，此时长木板C运动的位移为x2
对小物块B有
μmg＝maB，
v22－v2＝2aBx1
对长木板C有
μmg＝2maC，
v2＝2aCx2，
＝
木板的最小长度
L＝x1－x2
由以上各式解得
L＝.
练习册系列答案
相关题目
