题目内容
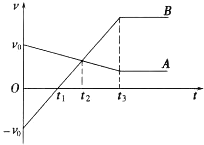
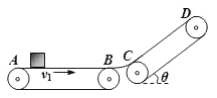
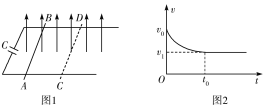
【题目】如图1所示，两平行长直光滑金属导轨水平放置，间距为L，左端连接一个电容为C的电容器，导轨处在磁感应强度大小为B、方向垂直导轨平面向上的匀强磁场中。质量为m的金属棒垂直导轨放置，某时刻金属棒获得一个水平向右的初速度v0，之后金属棒运动的v－t图象如图2所示。不考虑导轨的电阻。
(1)求金属棒匀速运动时的速度v1；
(2)求金属棒匀速运动时电容器的电荷量q；
(3)已知金属棒从开始到匀速运动的过程中，产生的焦耳热为Q，求电容器充电稳定后储存的电能E。
【答案】(1) 
(2)
(3)
－
－Q
【解析】
(1)金属棒匀速运动切割磁感线产生的电动势E=BLv1
电容器的电荷量q=CE
金属棒从开始到匀速运动的过程中，由动量定理有－B
Lt0=mv1－mv0
电容器的电荷量q=t0
联立解得v1=
(2)由(1)可知q=CE=CBLv1=
(3)在0～t时间内，金属棒的速度由v0到v1，由能量守恒可得E＋Q=
解得E=－
－Q
练习册系列答案
相关题目
