题目内容
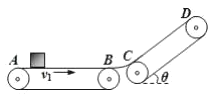
【题目】某工厂为实现自动传送工件设计了如图所示的传送装置,由一个水平传送带AB和倾斜传送带CD组成,水平传送带长度LAB=4m,倾斜传送带长度LCD=4.45m,倾角为θ=37°,AB和CD通过一段极短的光滑圆弧板过渡,AB传送带以v1=5m/s的恒定速率顺时针运转,CD传送带静止.已知工件与传送带间的动摩擦因数均为μ=0.5,重力加速度g=10m/s2.现将一个工件(可看作质点)无初速度地放在水平传送带最左端A点处,求:
(1)工件被第一次传送到CD传送带上升最大高度;
(2)若CD顺时针转动,要使物体能被传送到D端,求传送带的速度满足的关系,及物体从C到D所用的时间的取值范围。(sin37°=0.6,cos37°=0.8)
【答案】(1)![]() (2)传送带
(2)传送带![]() ,
,![]()
【解析】
(1)工件在水平传送带上运动过程,由牛顿第二定律得:![]()
解得:![]()
匀加速的位移:![]()
然后工件与水平传送带一起匀速运动,工件到达传送带CD时速度为5m/s;
工件在传送带CD上运动时,由牛顿第二定律得:![]()
代入数据解得:![]() ,
,
工件在CD上的位移:![]()
(2)传送带![]() ,在CD上,因为:
,在CD上,因为:![]() ,使滑块匀减速上滑
,使滑块匀减速上滑
由牛顿第二定律得:![]()
代入数据解得:![]()
由牛顿第二定律得:![]()
代入数据解得:![]()
速度关系为:![]()
可得:![]()
位移关系为:![]()
可得:![]()
联立解得:![]()
所以![]() ,
,![]()
若一直以![]() 匀减速
匀减速![]() ,即
,即![]() ,
,
解得:![]() (+舍去)
(+舍去)
所以![]()

练习册系列答案
相关题目