题目内容
【题目】如图所示，光滑导轨MN、PQ在同一水平面内平行固定放置，其间距d=1.0m，右端通过导线与阻值R=2.0Ω的电阻相连，在正方形区域CDGH内有竖直向下的匀强磁场。 一质量m=100g、阻值r=0.5Ω的金属棒，在与金属棒垂直、大小为F=0.2N的水平恒力作用下，从CH左侧x=1.0m处由静止开始运动，刚进入磁场区域时恰好做匀速直线运动。不考虑导轨电阻，金属棒始终与导轨垂直并保持良好接触. 求：
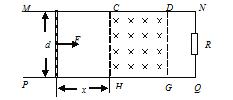
（1）匀强磁场磁感应强度B的大小；
（2）金属棒穿过磁场区域的过程中电阻R所产生的焦耳热；
（3）其它条件不变，如果金属棒进入磁场时立即撤掉恒力F，试讨论金属棒是否能越过磁场区域并简要说明理由；
（4）接（3）问，试求上述过程中流过电阻R的电量是多少。
【答案】(1) 
(2) 
(3)可以穿越 （4）
【解析】 (1)金属棒未进入磁场前做匀加速直线运动,由F=ma得：a=F/m=0.2/0.1m/s2=2m/s2.
进入磁场瞬间的速度为v,由v2=2ax得：v=2m/s.
金属棒进入磁场瞬间恰好做匀速运动，则有：
F=FA…①
FA=BId…②
I=E/(R+r)…③
E=Bdv…④
由①②③④联立解得：B= 0.5T.
(2)金属棒穿越磁场过程中产生的感应电流为：I=
=0.4A.
金属棒穿越磁场所用的时间为：t=d/v=1/2s=0.5s，
电阻R产生的焦耳热为：Q=I2Rt=0.42×2×0.5J=0.16J.
(3)设磁场区域无限长，金属棒在安培力作用下做减速运动，最后静止，将此过程无限分割，向右为正，由动量定理可得：
(BdI1△t1+BdI2△t2+BdI3△t3+…+BdIn△tn)=0mv，
(BdBdv1△t1+Bdv2△t2+BdBdv3△t3+…+BdBdvn△tn)/（R+r）=0mv，
，
代入数据解得：x′=2m>1m.
所以金属棒可以超过磁场区域右边界。
（4）根据q=(I1△t1+I2△t2+I3△t3+…+In△tn)= 
=
