题目内容
如图所示，一飞行器围绕地球沿半径为r的圆轨道1运动。经P点时，启动推进器短时间向前喷气使其变轨，2、3是与轨道1相切于P点的可能轨道。则飞行器( )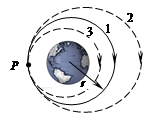
| A．变轨后将沿轨道2运动 |
| B．相对于变轨前运行周期变长 |
| C．变轨前、后在两轨道上经P点的速度大小相等 |
| D．变轨前、后在两轨道上经P点的加速度大小相等 |
D
解析试题分析：推进器短时间向前喷气，飞行器将被减速，故选项C错误；此时有：
＞
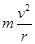，所以飞行器将做向心运动，即变轨后将沿较低轨道3运动，故选项A错误；根据开普勒第三定律可知，公转周期将变小，故选项B错误；由于变轨前、后在两轨道上经P点时，所受万有引力不变，因此加速度大小不变，故选项D正确。
考点：本题主要考查了万有引力定律的应用问题，属于中档偏低题。
考前必练系列答案目前我国已经成功发射北斗导航卫星十六颗，计划到2020年，将建成由35颗卫星组网而成的全球卫星导航系统，关于卫星网中的地球同步静止卫星，以下说法正确的是( )
| A．运行角速度相同 |
| B．环绕地球运行可以不在同一条轨道上 |
| C．运行速度大小相等，且都大于7.9km/s |
| D．向心加速度大于静止在赤道上物体的向心加速度大小 |
地球赤道地面上有一物体随地球的自转而做圆周运动，所受的向心力为F1，向心加速度为a1，线速度为v1，角速度为ω1；绕地球表面附近做圆周运动的人造卫星（高度忽略）所受的向心力为F2 ，向心加速度为a2，线速度为v2，角速度为ω2；地球同步卫星所受的向心力为F3 ，向心加速度为a3，线速度为v3 ，角速度为ω3；地球表面重力加速度为g ，第一宇宙速度为v ，假设三者质量相等，则下列结论正确的是 （ ）
| A．F1＝F2＞F3 | B．a1＝a2＝g＞a3 |
| C．v1＝v2＝v＞v3 | D．ω1＝ω3＜ω2 |
已知地球半径为R，月球半径为r，地球与月球之间的距离(两球中心之间的距离)为L。月球绕地球公转的周期为T1，地球自转的周期为T2，地球绕太阳公转周期为T3，假设公转运动都视为圆周运动，万有引力常量为G，由以上条件可知： （ ）
A．地球的质量为m地=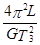 | B．月球的质量为m月= |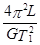
C．地球的密度为ρ=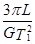 | D．月球运动的加速度为a= |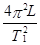
“天宫一号”被长征二号火箭发射后，准确进入预定轨道，如图所示，“天宫一号”在轨道1上运行4周后，在Q点开启发动机短时间加速，关闭发动机后，“天宫一号”沿椭圆轨道2运行到达P点，开启发动机再次加速，进入轨道3绕地球做圆周运动，“天宫一号”在图示轨道1、2、3上正常运行时，下列说法正确的是( )．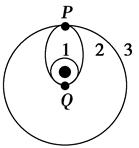
| A．“天宫一号”在轨道3上的速率大于在轨道1上的速率 |
| B．“天宫一号”在轨道3上的角速度大于在轨道1上的角速度 |
| C．“天宫一号”在轨道1上经过Q点的加速度大于它在轨道2上经过Q点的加速度 |
| D．“天宫一号”在轨道2上经过P点的加速度等于它在轨道3上经过P点的加速度 |
关于做匀速圆周运动的地球人造卫星的下列说法中正确的是
| A．卫星运行可以经过广州正上空 |
B．卫星运行的速度可能达到 |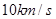
C．离地面高为R（R为地球半径）处的卫星加速度为 |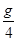
| D．卫星中的物体处于完全失重状态，所以物体不受重力。 |
2013年6月13日，我国“神舟十号”与“天宫一号”成功实现交会对接，如图所示圆形轨道Ⅰ为“天宫一号”运行轨道，圆形轨道Ⅱ为“神舟十号”运行轨道，在实现交会对接前，“神舟十号”要进行多次变轨，则（ ）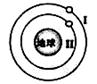
| A．“神舟十号”在圆形轨道Ⅱ的运行速率大于7．9km/s |
| B．“天宫一号”的运行速率小于“神舟十号”在轨道Ⅱ上的运行速率 |
| C．“神舟十号”变轨前后机械能守恒 |
| D．“天宫一号”的向心加速度大于“神舟十号” 在轨道Ⅱ上的向心加速度 |
人造卫星绕地球只受地球的引力，做匀速圆周运动，其轨道半径为r，线速度为v，周期为T。为使其周期变为8T，可采用的方法有
| A．保持轨道半径不变，使线速度减小为v/8 |
| B．逐渐减小卫星质量，使轨道半径逐渐增大为4r |
| C．逐渐增大卫星质量，使轨道半径逐渐增大为8r |
| D．保持线速度不变v，将轨道半径增加到8r |