Question

如图所示，在水平面上固定三个完全相同的木块，一颗子弹以水平速度v射入，若子弹在木块中做匀减速直线运动，当穿透第三块木块时速度恰好为零，则子弹依次射入每个木块时的速度之比和穿过每个木块所用时间之比分别为（　　）

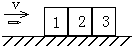
A．v1：v2：v3=3：2：1	B．v1：v2：v3= 3 ： 2 ：1
C．t1：t2：t3=1： 2 ： 3	D．t1：t2：t3=( 3 - 2 )：( 2 -1)：1

Answer 1

C、D、子弹匀减速穿过三木块，末速度为零，我们假设子弹从右向左作初速度为零的匀加速直线运动．
则：子弹依次穿过321三木块所用时间之比：t3：t2：t1=1：(

2

-1)：(

3

-

2

)；
得：子弹依次穿过123三木块所用时间之比：t1：t2：t3=(

3

-

2

)：(

2

-1)：1； 故C错误，D正确．
A、B、设子弹穿过第三木块所用时间为1秒，则穿过3，2两木块时间为：t3+t2=

2

秒，穿过3，2，1三木块时间为：t3+t2+t1=

3

s
则：子弹依次穿过3，2，1三木块时速度之比为：1：

2

：

3

；
所以，子弹依次穿过1，2，3三木块时速度之比为：

3

：

2

：1；故A错误，B正确．
故选：BD