题目内容
2.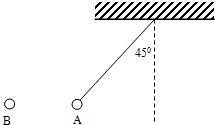 如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时
如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时(1)小球B受到的库仑力F为多少?
(2)小球A带何种电荷?所带电荷量为多少?(g=10m/s2)
分析 对小球A进行正确受力分析,小球受水平向左的库仑力、重力、绳子的拉力,根据平衡条件列方程求解库仑力大小;
再依据库仑定律的公式,即可求解小球A电量,同时根据同种电荷相斥,异种电荷相吸,即可求解.
解答 解:(1)小球受水平向左的库仑力、重力、绳子的拉力而平衡,根据平衡条件有:
F库=mgtanθ…①
F库=k$\frac{{q}_{A}{q}_{B}}{{r}^{2}}$…②
将r=3cm=0.03m,θ=45°
代入解①②得:F库=2×10-3N,
(2)根据第(1)题,解得:qA=5×10-9 C.
故根据牛顿第三定律可知,B所受库仑引力为2×10-3N,小球A带的电量是5×10-9C.由于B带正电,故A带负电.
答:(1)此时小球B受到的库仑力F是2×10-3 N.
(2)小球A带负电,电量是5×10-9 C.
点评 本题结合物体平衡考查了库仑定律的应用,属于简单基础题目,是一道考查基础知识的好题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
10.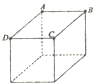 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )| A. | $\sqrt{2}$N | B. | 2$\sqrt{2}$N | C. | 3.6$\sqrt{2}$N | D. | 3.6$\sqrt{3}$N |
7.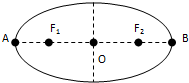 某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
 某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )| A. | F1点 | B. | F2点 | C. | O点 | D. | 均不正确 |
14.关于太阳系中行星的说法不正确的是( )
| A. | 行星绕太阳运动的轨道都是椭圆,太阳在椭圆的一个焦点上 | |
| B. | 离太阳越远的行星上的“一年”时间越长 | |
| C. | 木星的轨道半径大于地球的轨道半径,故木星上的重力加速度小于地球上的重力加速度 | |
| D. | 木星的轨道半径大于地球的轨道半径,故木星公转的向心加速度小于地球公转的向心加速度 |
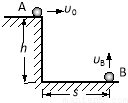 如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度v0应大于$s\sqrt{\frac{g}{2h}}$,A、B两球初速度之比$\frac{{v}_{0}}{{v}_{B}}$为$\frac{s}{h}$.
如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度v0应大于$s\sqrt{\frac{g}{2h}}$,A、B两球初速度之比$\frac{{v}_{0}}{{v}_{B}}$为$\frac{s}{h}$. 当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg )
当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg ) 如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.
如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.