题目内容
17.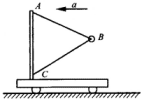 如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.
如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.
分析 当BC绳拉直但没有力时,AB绳子拉力的水平分力产生加速度,AB绳拉力的竖直分力和重力平衡,根据牛顿第二定律列式求出此时的加速度,当两绳均有力时,对球受力分析,竖直方向受力平衡,求出两绳拉力之差.
解答 解:当BC绳刚开始有拉力时,绳子绷紧,拉力恰好为零,对小球受力分析如图所示:
水平方向:${T}_{1}^{\;}sin60°=ma$①
${T}_{1}^{\;}cos60°=mg$②
联立①②得:$a=\sqrt{3}g$
当两根绳子均有拉力时,受力分析如图所示: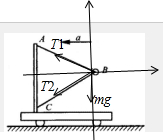
运用正交分解法:竖直方向受力平衡
${T}_{1}^{\;}cos60°={T}_{2}^{\;}cos60°+mg$③
由③得:$△T={T}_{1}^{\;}-{T}_{2}^{\;}=2mg$
故答案为:$\sqrt{3}$g,2mg.
点评 解决本题的关键知道小球和小车具有相同的加速度,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6.位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动,F1的功率为P1;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,F2的功率为P2..已知v1<v2.则P1、P2.的关系正确的是( )

| A. | P1=P2 | B. | P1<P2 | C. | P1>P2 | D. | 无法比较 |
8.真空中有两个相同的带电金属小球A和B,相距为r,带电量分别为q和2q,它们之间相互作用力的大小为F.有一个不带电的金属球C,大小跟A、B相同,当C跟A、B小球各接触一次后拿开,再将A、B间距离变为2r,那么A、B间的作用力的大小可为( )
| A. | $\frac{3F}{64}$ | B. | 0 | C. | $\frac{3F}{32}$ | D. | $\frac{3F}{16}$ |
5.真空中有两个异种点电荷A、B,若A固定,在B逐渐靠近A的过程中,则两电荷间的库仑力将( )
| A. | 先增大后减小 | B. | 不断增大 | C. | 保持不变 | D. | 不断减小 |
9.关于地球的第一宇宙速度,下列说法正确的是( )
| A. | 它是人造地球卫星绕地球运行的最小速度 | |
| B. | 它是近地圆轨道上人造地球卫星的运行速度 | |
| C. | 它是能使卫星进入近地轨道的最大发射速度 | |
| D. | 它是同步卫星绕地球运行的速度 |
7. 如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
 如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )| A. | E=$\frac{F}{q}$,方向水平向左 | B. | E=$\frac{F}{q}$,方向水平向右 | ||
| C. | E=$\frac{F}{Q}$,方向水平向左 | D. | E=$\frac{F}{Q}$,方向水平向右 |

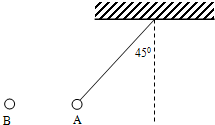 如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时
如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时