题目内容
12.子弹以600m/s的初速度击中一静止在光滑水平面上的木块,经过0.05s穿出木块,子弹的速度变为200m/s,则子弹穿过木块时加速度大小为8000m/s2,方向与子弹的初速度方向相反;若木块在此过程产生了200m/s2的加速度,则木块获得速度大小为10m/s.分析 根据匀变速直线运动的速度时间公式求出子弹的加速度大小.根据速度时间公式求出木块获得的速度.
解答 解:子弹穿过木块时子弹的加速度大小a1=$\frac{{v}_{2}-{v}_{1}}{t}$=$\frac{200-600}{0.05}$m/s2=-8000m/s2,
负号说明子弹做减速运动,故方向与子弹的初速度方向相反;
木块做匀加速直线运动,故0.05s末获得的速度v=at=200×0.05m/s=10m/s.
故答案为:8000m/s2.与子弹的初速度方向相反; 10m/s.
点评 本题考查匀变速直线运动规律的应用,解决本题的关键掌握匀变速直线运动的速度时间公式,并能灵活运用,基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
3.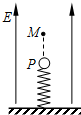 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )| A. | 小球电势能的减少量大于小球重力势能的增加量 | |
| B. | 弹簧弹性势能的增加量等于小球动能的减少量 | |
| C. | 小球机械能的改变量等于电场力做的功 | |
| D. | 小球动能的减少量等于电场力和重力做功的代数和 |
20.下列有关科学家的贡献说法正确的是( )
| A. | 卡文迪许发现了万有引力定律 | |
| B. | 奥斯特首先提出用电场线来描绘电场 | |
| C. | 密立根通过对摩擦起电的研究测定了元电荷的电荷量 | |
| D. | 麦克斯韦建立了电磁场理论,并提出光也是一种电磁波 |
7. 如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
 如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )
如图,在电荷量为Q的点电荷产生的电场中,电荷量为q的负检验电荷在A点受到的电场力为F.方向水平向左.则A点的电场强度( )| A. | E=$\frac{F}{q}$,方向水平向左 | B. | E=$\frac{F}{q}$,方向水平向右 | ||
| C. | E=$\frac{F}{Q}$,方向水平向左 | D. | E=$\frac{F}{Q}$,方向水平向右 |
17. 如图所示,轻弹簧的一端固定在墙上,另一端与质量为m的物体A栓接在一起,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,物体A向右运动,之后物体A沿水平面往复运动.最终物体A停在初始位置.已知弹簧始终在弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,轻弹簧的一端固定在墙上,另一端与质量为m的物体A栓接在一起,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,物体A向右运动,之后物体A沿水平面往复运动.最终物体A停在初始位置.已知弹簧始终在弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
 如图所示,轻弹簧的一端固定在墙上,另一端与质量为m的物体A栓接在一起,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,物体A向右运动,之后物体A沿水平面往复运动.最终物体A停在初始位置.已知弹簧始终在弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,轻弹簧的一端固定在墙上,另一端与质量为m的物体A栓接在一起,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,物体A向右运动,之后物体A沿水平面往复运动.最终物体A停在初始位置.已知弹簧始终在弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )| A. | 物体A整个运动过程,弹簧弹力的冲量为零 | |
| B. | 物体A运动时间t=$\frac{{I}_{0}}{μmg}$ | |
| C. | 物体A通过的总路程s=$\frac{{I}_{0}^{2}}{2μg{m}^{2}}$ | |
| D. | 在物体A整个运动过程中,弹簧对物体A做功为零. |
7.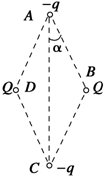 如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
 如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )| A. | cos3 α=$\frac{q}{8Q}$ | B. | cos3 α=$\frac{{q}^{2}}{{Q}^{2}}$ | C. | sin3 α=$\frac{Q}{8q}$ | D. | sin3 α=$\frac{{Q}^{2}}{{q}^{2}}$ |
4. 在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
 在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )| A. | 正电,在A、B之间 | B. | 正电,在B点右侧 | C. | 负电,在B点右侧 | D. | 负电,在A点左侧 |
5.在一次抗洪抢险中,抢险队员驾驶冲锋舟准备度过某河.已知该河宽80m,河中各点的河水速度大小与该点到河岸的距离成正比,冲锋舟在静水中的速度恒为4m/s,且渡河过程中,河水速度大小将随上游降雨量的变化而变化.关于上述渡河过程,下列说法正确的是( )
| A. | 抢险队员到达对岸的最短时间是20s,这一时间与河水速度大小是否变化无关 | |
| B. | 随着河水速度大小的变化,船到达对岸的最短时间会相应变化 | |
| C. | 若冲锋舟的船头始终垂直于河岸,当它距离岸40m处的河水速度大小是3m/s,则此时船的实际速度是5m/s | |
| D. | 无论河水速度多大,也无论抢险队员怎样调整船的航向,冲锋舟都无法到达河对岸 |
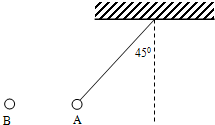 如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时
如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时