Question

【题目】如图所示，一质量为M的斜面静止在水平地面上，物体B受沿斜面向上力F作用沿斜面匀速上滑，A、B之间动摩擦因数为μ，μ＜tanθ，且质量均为m，则（ ）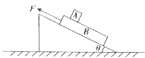

A.A，B保持相对静止
B.地面对斜面体的摩擦力等于mg（sinθ﹣μcosθ）cosθ+Fcosθ
C.地面受到的压力等于（M+2m）g
D.B与斜面间动摩擦因数为

Answer 1

【答案】B,D
【解析】解：A、对A分析，因为μ＜tanθ，则mgsinθ＞μmgcosθ，则A、B不能保持相对静止，A不符合题意．

B、以AB为研究的对象，A受到重力、支持力、和斜面体B对A的摩擦力，

垂直于斜面的方向：N=mgcosα

沿斜面的方向：mgsinα﹣μN=ma

由于μ＜tanα，则：ma=mgsinα﹣μmgcosα＞0

加速度aA=gsinθ﹣μgcosθ，

将B和斜面体视为整体，受力分析

可知地面对斜面体的摩擦力等于m（gsinθ﹣μgcosθ）cosθ+Fcosθ，地面受到的压力为（M+2m）g﹣Fsinθ﹣m（gsinθ﹣μgcosθ）sinθ，B符合题意，C不符合题意．

D、B与斜面体的正压力N=2mgcosθ，对B分析，根据共点力平衡有：F=mgsinθ+μmgcosθ+f′，

则动摩擦因数 ．D符合题意．

答案为：BD．
【考点精析】掌握滑动摩擦力和静摩擦力是解答本题的根本，需要知道滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解；静摩擦力:静摩擦力大小可在0与fmax 之间变化，一般应根据物体的运动状态由平衡条件或牛顿定律来求解．