题目内容
【题目】如图所示为某种弹射装置的示意图,光滑的水平导轨MN高h=0.8 m,右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮带动皮带以v=3.0 m/s的速度沿顺时针方向匀速传动.三个质量均为m=l.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,其间有一压缩的轻弹簧,处于静止状态.滑块A以初速度vo=2.0 m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度vc=2.0 m/s滑上传送带,并从右端滑m落至地面上的P点.已知滑块C与传送带之间的动摩擦因数μ=0. 20,重力加速度g取10 m/s2.求:
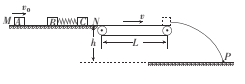
(1)P点到传送带右端的水平距离s;
(2)滑块B、C用细绳相连时弹簧的弹性势能E。;
(3)若弹簧的压缩情况不变,要使滑块C总能落至P点,则滑块A与滑块B碰撞前速度的最大值vm是多少?
【答案】(1)1.2m(2)1.0J(3)7.1m/s
【解析】
弹性碰撞中在满足动量守恒的同时还满足机械能守恒及碰撞中的能量保持不变;本题中AB碰撞后在弹簧伸开的过程中同时满足动量守恒和机械能守恒。
物体滑上传送带后,如果物体的速度大于传送带的速度则物体将在摩擦力的作用下做减速运动,减速运动持续到物体到达传送带的另一端或速度降为和传送带同速时止,解题时要注意判断;如果物体的速度小于传送带的速度则物体将在摩擦力的作用下作匀加速运动,加速运动持续到物体到达传送带的另一端或速度加到与传送带同速时止,解题时同样要注意判断。
(1) 滑块C滑上传送带后做匀加速运动,设滑块C从滑上传送带到速度达到传送带的速度v所用的时间为t,加速度大小为a,在时间t内滑块C的位移为x。
根据牛顿第二定律和运动学公式
μmg=ma
v=vC+at
![]()
代入数据可得 x=1.25m
∵x=1.25m<L
即滑块C在传送带上先加速到传送带速度后再随传送带匀速运动,并从右端以v=3m/s的速度滑出做平抛运动,则有:
![]()
![]()
解得:s=1.2m;
(2) 设A、B碰撞后的速度为v1,A、B与C分离时的速度为v2,由动量守恒定律
mAv0=(mA+mB)v1
(mA+mB)v1=(mA+mB)v2+mCvC
AB碰撞后,弹簧伸开的过程系统能量守恒
![]()
代入数据可解得:EP=1.0J;
(3) 在题设条件下,若滑块A在碰撞前速度有最大值,则碰撞后滑块C的速度有最大值,它减速运动到传送带右端时,速度应当恰好等于传递带的速度v。设A与B碰撞后的速度为v1′,分离后A与B的速度为v2′,滑块C的速度为vc′,
根据动量守恒定律可得:
AB碰撞时:![]()
弹簧伸开时:![]()
在弹簧伸开的过程中,系统能量守恒:
![]()
∵C在传送带上做匀减速运动的末速度为v=3m/s,加速度大小为2m/s2
∴由运动学公式![]() 解得:
解得:![]()
代入数据联列方程解得:![]() 。
。

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案