题目内容
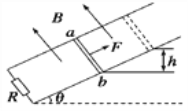
【题目】如图所示，在一个边长为a的正六边形区域内存在磁感应强度为B，方向垂直于纸面向里的匀强磁场．三个相同带正电的粒子，比荷为q/m ，先后从A点沿AD方向以大小不等的速度射入匀强磁场区域，粒子在运动过程中只受磁场力作用．已知编号为①的粒子恰好从F点飞出磁场区域，编号为②的粒子恰好从E点飞出磁场区域，编号为③的粒子从ED边上的某一点垂直边界飞出磁场区域．求：
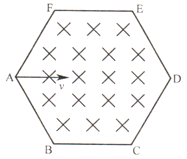
（1）编号为①的粒子进入磁场区域的初速度大小；
（2）编号为②的粒子在磁场区域内运动的时间；
（3）编号为③的粒子在ED边上飞出的位置与E点的距离．
【答案】（1）
（2）
（3）
【解析】
作出运动轨迹，结合几何知识求出三种粒子的半径，然后根据牛顿第二定律求出粒子的速度，结合周期公式和几何知识求解所要求的物理量。
（1）设编号为①的粒子在正六边形区域磁场中做圆周运动的半径为r1，初速度大小为v1，则有：qv1B=m
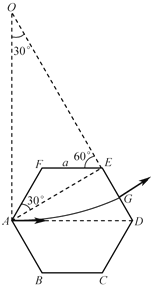
由几何关系可得：r1=
解得：v1=
（2）设编号为②的粒子在正六边形区域磁场中做圆周运动的半径为r2，线速度大小为v2，周期为T2，则：qv2B=m
T2=
解得：T2=
由几何关系可得，粒子在正六边形区域磁场运动过程中，转过的圆心角为60°，则粒子在磁场中运动的时间：
（3）设编号为③的粒子在正六边形区域磁场中做圆周运动的半径为r3，由几何关系可得：AE=2acos30°=
a 
OE=
=3a
EG=r3-OE=（2-3）a
第1卷单元月考期中期末系列答案
【题目】下表是一辆电动自行车的部分技术指标，其中额定车速是指电动自行车满载情况下在水平平直道路上以额定功率匀速行驶的速度。
额定车速 | 整车质量 | 载重 | 额定输出功率 | 电动机额定工作电压和电流 |
18km/h | 40kg | 80kg | 180W | 36V/6A |
请参考表中数据，完成下列问题 (g取10 m/s2)：
（1）此电动机的电阻是多少？正常工作时，电动机的效率是多少？
（2） 在水平平直道路上行驶过程中电动自行车受阻力是车重（包括载重）的k倍，试计算k的大小。
（3）仍在上述道路上行驶，若电动自行车满载时以额定功率行驶，当车速为2m/s时的加速度为多少？
