题目内容
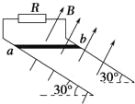
【题目】光滑的平行金属导轨长L=2m，两导轨间距d=0.5m，轨道平面与水平面的夹角θ=30°，导轨上端接一阻值为R=0.6Ω的电阻，轨道所在空间有垂直轨道平面向上的匀强磁场，磁场的磁感应强度B=1T，如图所示．有一质量m=0.5kg、电阻r=0.4Ω的金属棒ab，放在导轨最上端，其余部分电阻不计．已知棒ab从轨道最上端由静止开始下滑到最底端脱离轨道的过程中，电阻R上产生的热量Q1=0.6J，取g=10m/s2，则下列说法正确的是（ ）
A. 棒下滑到轨道最底端时加速度的大小为3m/s2
B. 当棒的速度v=2m/s时，电阻R两端的电压为0.4V
C. 棒下滑到轨道最底端时速度的大小为2m/s
D. 当棒的速度v=2m/s时，电阻R两端的电压为1.0V
【答案】A
【解析】
AC．整个过程，根据焦耳定律：
，所以两电阻上产热之比为3：2，所以金属棒产热为：
，根据能量守恒有：
，解得到最底端速度：
，此时感应电动势：
，感应电流:
，安培力：
，根据牛顿第二定律：
联立解得：
，A正确C错误。
BD．当棒的速度v=2m/s时，
，此时回路电流:
，电阻R两端的电压为:
，BD错误。
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
