题目内容
如图所示，光滑斜面的倾角为θ，斜面上放一光滑档板AB，档板与斜面间放一质量为m的小球，档板可以以B点为轴线转动，直至水平，在转动过程中球对档板压力的最小值为 ，球对斜面压力的最小值为 ．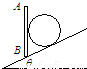
【答案】分析：以小球为研究对象，在挡板所受的三个力中，重力大小方向都不变，斜面支持力方向不变，三力的合力始终为零，作出几个有代表性的图进行分析．
解答：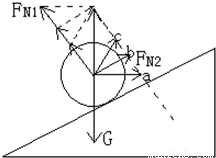
解：以小球为研究对象，进行受力分析如图，将FN1与FN2合成，其合力与重力等大反向，则在挡板转动时，挡板给球的弹力FN2与斜面给球的弹力FN1合力大小、方向均不变，其中FN1的方向不变，作辅助图如图，挡板转动过程中，FN2的方向变化如图中a、b、c的规律变化，为满足平行四边形定则，其大小变化规律为先减小后增大，其中挡板与斜面垂直时FN2最小．斜面对球的作用力FN1一直减小，当挡板水平时，斜面对球的支持力最小，为零．
再根据牛顿第三定律得，在该过程中，球对挡板的压力方向始终与挡板垂直指向挡板，大小先减小后增大，当挡板与斜面垂直时FN2最小，最小值为mgsinθ．球对斜面压力的最小值为零．
故答案为：mgsinθ，0
点评：本题关键是对小球受力分析，然后根据平衡条件并运用合成法分析；要明确三力平衡中，任意两个力的合力与第三个力等值、反向、共线．
解答：
解：以小球为研究对象，进行受力分析如图，将FN1与FN2合成，其合力与重力等大反向，则在挡板转动时，挡板给球的弹力FN2与斜面给球的弹力FN1合力大小、方向均不变，其中FN1的方向不变，作辅助图如图，挡板转动过程中，FN2的方向变化如图中a、b、c的规律变化，为满足平行四边形定则，其大小变化规律为先减小后增大，其中挡板与斜面垂直时FN2最小．斜面对球的作用力FN1一直减小，当挡板水平时，斜面对球的支持力最小，为零．再根据牛顿第三定律得，在该过程中，球对挡板的压力方向始终与挡板垂直指向挡板，大小先减小后增大，当挡板与斜面垂直时FN2最小，最小值为mgsinθ．球对斜面压力的最小值为零．
故答案为：mgsinθ，0
点评：本题关键是对小球受力分析，然后根据平衡条件并运用合成法分析；要明确三力平衡中，任意两个力的合力与第三个力等值、反向、共线．
练习册系列答案
相关题目
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
（2011?温州二模）如图所示，光滑绝缘水平面AB与倾角θ=370，长L=6m的绝缘斜面BC在B处圆滑相连，在斜面的C处有一与斜面垂直的弹性绝缘挡板，质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D，整个空间存在水平向右的匀强电场，场强E=2xlO5N/C，现让滑块以v0=12m/s的速度沿斜面向上运动．设滑块与挡板碰撞前后所带电荷量不变、速度大小不变，滑块和斜面间的动摩擦因数μ=0.1，求：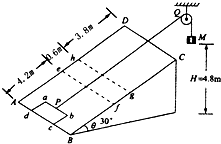
如图所示，光滑矩形斜面ABCD的倾角θ=30°，在其上放置一矩形金属线框abcd，ab的边长l1=1m，bc的边长l2=0.6m，线框的质量m=1kg，电阻R=0.1Ω，线框通过细线绕过定滑轮与重物相连，细线与斜面平行且靠近；重物质量M=2kg，离地面的高度为H=4.8m；斜面上efgh区域是有界匀强磁场，方向垂直于斜面向上；已知AB到ef的距离为S1=4.2m，ef到gh的距离S2=0.6m，gh到CD的距离为S3=3.8m，取g=10m/s2；现让线框从静止开始运动（开始时刻，cd与AB边重合），发现线框匀速穿过匀强磁场区域，求：