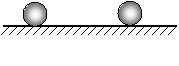题目内容
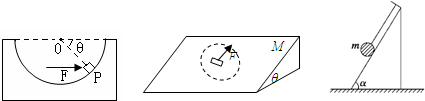
(1)如图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用下静止P点.设滑块所受支持力为FN.OF与水平方向的夹角为θ.则F=
,FN=
.
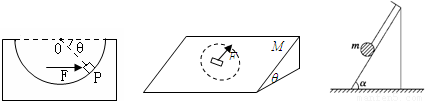
(2)一质量为M、倾角θ为的斜面体在水平地面上,质量为m的小木块(可视为质点)放在斜面上,现用一平行于斜面的、大小恒定的拉力F作用于小木块,拉力在斜面所在的平面内绕小木块旋转一周的过程中,斜面体和木块始终保持静止状态,则小木块受到斜面的最大摩擦力为
(3).如图所示,倾角α=60°的光滑斜面体上有一个小球m被平行于斜面的细绳系于斜面上,斜面体放在水平面上.当斜面体以a=g的水平加速度向右作匀加速运动时,绳上的拉力为
mg
mg.

| mg |
| tanθ |
| mg |
| tanθ |
| mg |
| sinθ |
| mg |
| sinθ |
(2)一质量为M、倾角θ为的斜面体在水平地面上,质量为m的小木块(可视为质点)放在斜面上,现用一平行于斜面的、大小恒定的拉力F作用于小木块,拉力在斜面所在的平面内绕小木块旋转一周的过程中,斜面体和木块始终保持静止状态,则小木块受到斜面的最大摩擦力为
F+mgsinθ
F+mgsinθ
,斜面体受到地面的最大摩擦力为F
F
.(3).如图所示,倾角α=60°的光滑斜面体上有一个小球m被平行于斜面的细绳系于斜面上,斜面体放在水平面上.当斜面体以a=g的水平加速度向右作匀加速运动时,绳上的拉力为
| 2 |
| 2 |

分析:(1)1、2两题可分别选研究对象,受力分析应用平衡条件求解.
(2)第3题:需要对小球进行受力分析后判断小球是飞起来还是仍能压在斜面上.
(2)第3题:需要对小球进行受力分析后判断小球是飞起来还是仍能压在斜面上.
解答:解:(1)对滑块受力分析并合成如图:
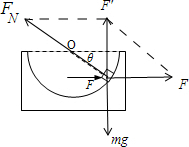
由平衡条件:F′=mg
由三角函数:sinθ=
,得:FN=
tanθ=
,得:F=
(2)当F沿斜面向下时,木块所受摩擦力最大,受力分析如图:

由平衡条件:fMAX=F+mgsinθ
选整体为研究对象,当F水平时,整体所受的摩擦力最大,由平衡条件,f=F,即:斜面所受的最大静摩擦力为F
(3)假设物体刚要离开斜面时,即:斜面对球无支持力,设此时加速度为a
受力分析如图:
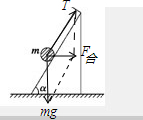
F合=
,所以a=
=
g<g
故当加速度为g时,小球已经飞起来,小球受力分析如图:
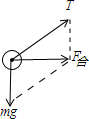
因为加速度为g,故:F合=mg
在直角三角形中:T=
=
mg
故答案为:(1)
;
(2)F+mgsinθ;F
(3)
mg

由平衡条件:F′=mg
由三角函数:sinθ=
| mg |
| FN |
| mg |
| sinθ |
tanθ=
| mg |
| F |
| mg |
| tanθ |
(2)当F沿斜面向下时,木块所受摩擦力最大,受力分析如图:

由平衡条件:fMAX=F+mgsinθ
选整体为研究对象,当F水平时,整体所受的摩擦力最大,由平衡条件,f=F,即:斜面所受的最大静摩擦力为F
(3)假设物体刚要离开斜面时,即:斜面对球无支持力,设此时加速度为a
受力分析如图:

F合=
| mg |
| tanα |
| mg | ||
m
|
| ||
| 3 |
故当加速度为g时,小球已经飞起来,小球受力分析如图:

因为加速度为g,故:F合=mg
在直角三角形中:T=
(mg)2+
|
| 2 |
故答案为:(1)
| mg |
| tanθ |
| mg |
| sinθ |
(2)F+mgsinθ;F
(3)
| 2 |
点评:受力平衡类的题目选择好研究对象后受力分析后应用平衡条件列式求解即可,关键是第3题和牛顿运动定律结合在一起,还需要判断是否小球飘起来,难度不小,需要细细体会.

练习册系列答案
相关题目