题目内容
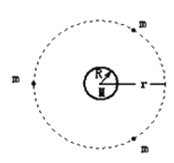
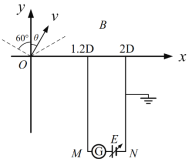
【题目】如图所示,在![]() 区域存在方向垂直
区域存在方向垂直![]() 平面向里、大小为B的匀强磁场.坐标原点处有一电子发射源,单位时间发射n个速率均为v的电子,这些电子均匀分布于
平面向里、大小为B的匀强磁场.坐标原点处有一电子发射源,单位时间发射n个速率均为v的电子,这些电子均匀分布于![]() 平面y轴两侧角度各为60°的范围内.在x轴的正下方放置平行于y轴、足够长的金属板M和N(极板厚度不计),两板分别位于
平面y轴两侧角度各为60°的范围内.在x轴的正下方放置平行于y轴、足够长的金属板M和N(极板厚度不计),两板分别位于![]() 和
和![]() 处,N板接地,两板间通过导线连接有电动势U在
处,N板接地,两板间通过导线连接有电动势U在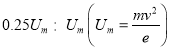 范围内可调节的电源E和灵敏电流计G.沿y轴正方向入射的电子,恰好能从
范围内可调节的电源E和灵敏电流计G.沿y轴正方向入射的电子,恰好能从![]() 处进入极板间.整个装置处于真空中,不计重力,忽略电子间的相互作用.
处进入极板间.整个装置处于真空中,不计重力,忽略电子间的相互作用.
(1)求电子的比荷;
(2)求电子在磁场中飞行的时间与发射角度![]() (速度方向与y轴的角度)的关系;
(速度方向与y轴的角度)的关系;
(3)通过计算,定性画出流过灵敏电流计G的电流i和电动势U的关系曲线.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据洛伦兹力提供向心力:![]()
根据其中题意可知半径为:r=D
联立可得:
![]()
(2)粒子的运动周期为:![]()
根据几何关系可知,当粒子从y轴的右侧射入时,对应的圆心角为:![]()
对应的时间为:
![]()
当粒子从y轴的左侧射入时,对应的圆心角为:![]()
对应的时间为:
![]()
(3)设进入![]() 极板电子所对应的最大发射角为
极板电子所对应的最大发射角为![]() ,则有
,则有![]() .
.![]()
左侧电子单位时间内能打到![]() 极板的电子数为:
极板的电子数为:![]()
对右侧电子:![]() 均能达到M板上,
均能达到M板上,![]() 以
以![]() 角射出恰好不能到达N板.
角射出恰好不能到达N板.
则有:![]()
电压为:
![]()
最大值为:![]()
最小值为:![]()
当![]() ,右侧所有电子均到达M板,饱和电流为:
,右侧所有电子均到达M板,饱和电流为:
![]()
当![]()
右侧角度小于![]() 电子均不能到达
电子均不能到达![]() 板,此时到达极板
板,此时到达极板![]() 的电子数为
的电子数为![]() .
.
灵敏电流计G的电流i和电动势U的关系曲线为:


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目