题目内容

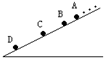相同的小球从斜面的某一位置每隔0.1s释放一颗，连续放了好几颗后，对斜面上正运动着的小球拍下部分照片，如图所示，现测得AB=15cm，BC=20cm，已知小球在斜面上做加速度相同的匀加速直线运动（初速度为零），则：拍片时，A球上方正运动的球有几个？（　　）
分析：匀变速直线运动在连续相等时间内的位移差为一恒量即△x=aT2，求出小球的加速度a；根据中间时刻的瞬时速度等于全程的平均速度可以求出B球的瞬时速度v，由于小球无初速释放，根据v=v0+at，可得小球从释放到B的时间，每隔0.1s释放一个小球可以知道A球上方正在运行的小球．
解答：解：对于匀变速直线运动有△x=aT2可得小球下滑的加速度a=
△x
T2
=
BC-AB
0．12
m/s2=
0.2-0.15
0．12
m/s2=5m/s2
又因为vB=
AC
2T
=
0.2+0.15
0.2
m/s=1.75m/s
故B球运动的时间tB=
vB
a
=
1.75
5
s=0.35s
故B球上方有3个球即A球上方有2个球．
故选C．
点评：解决本题的关键主要是匀变速直线运动的两个重要推论：（1）△x=aT2；（2）某段时间中间时刻的瞬时速度等于全程的平均速度v
t
2
=
.
v
．
练习册系列答案
相关题目
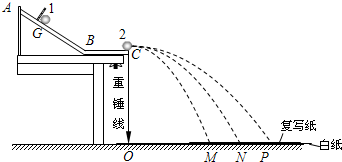某同学用如图所示的装置，利用两个大小相同的小球做对心碰撞来验证动量守恒定律，图中AB是斜槽，BC是水平槽，它们连接平滑，O点为重锤线所指的位置．实验时先不放置被碰球2，让球1从斜槽上的某一固定位置G由静止开始滚下，落到位于水平地面的记录纸上，留下痕迹，重复10次．然后将球2置于水平槽末端，让球1仍从位置G由静止滚下，和球2碰撞．碰后两球分别在记录纸上留下各自的痕迹，重复10次．实验得到小球的落点的平均位置分别为 M、N、P．
（1）在此实验中，球1的质量为m1，球2的质量为m2，需满足m1
大于
大于
 m2（选填“大于”、“小于”或“等于”）．
（2）被碰球2飞行的水平距离由图中线段
.
OP
.
OP
表示．
（3）若实验结果满足m1?
.
ON
=
m1?
.
OM
+m2?
.
OP
m1?
.
OM
+m2?
.
OP
，就可以验证碰撞过程中动量守恒．
在验证动量守恒定律实验中，同学们不仅完成了课本原来的实验，还用相同的器材进行多方面的探索及尝试．下面是甲、乙两组同学的实验，请回答相关的问题：
（Ⅰ）甲组同学采用如图1所示的装置，由斜槽和水平槽构成．将复写纸与白纸铺在水平放的木板上，重垂线所指的位置为O．实验时先使a球从斜槽上某一固定位置由静止开始滚下，落到位于水平地面的记录纸上，留下痕迹．重复上述操作多次，得到多个落点痕迹平均位置P；再把b球放在水平槽上靠近槽末端的地方，让a球仍从固定位置由静止开始滚下，与b球发生对心正碰，碰后a球不被反弹．碰撞后a、b球分别在记录纸上留下各自的落点痕迹．重复这种操作多次得到多个落点痕迹平均位置M、N．
（1）若a球质量为m1，半径为r1；b球质量为m2，半径为r2．则
C
C

A．m1＞m2　r1＞r2    B．m1＞m2　r1＜r2
C．m1＞m2　r1=r2     D．m1＜m2　r1=r2
（2）以下提供的器材中，本实验必需的有
AC
AC

A．刻度尺   B．打点计时器    C．天平   D．秒表
（3）设a球的质量为m1，b球的质量为m2，则本实验验证动量守恒定律的表达式为（用m1、m2、OM、OP、ON表示）
m1OP=m1OM+m2ON
m1OP=m1OM+m2ON

（Ⅱ）乙组同学误将重锤丢失，为了继续完成实验则将板斜放，上端刚好在槽口抛出点，标记为O．板足够长小球都能落在板上，如图2，采用甲组同学相同的操作步骤完成实验．
（4）对该组同学实验的判断正确的是
BD
BD

A．乙组同学无法完成验证动量守恒定律
B．秒表也不是乙组同学的必需器材
C．乙组同学必须测量斜面倾角θ
D．图2中N为b球碰后落点
（5）设a球的质量为m1，b球的质量为m2，则本实验验证动量守恒定律的表达式为
m1
OP
=m1
OM
+m2
ON
m1
OP
=m1
OM
+m2
ON
．
（6）如果a，b球的碰撞是弹性碰撞，那么还应满足的表达式为
m1OP=m1OM+m2ON
m1OP=m1OM+m2ON
． （要求第（5）（6）结论用m1、m2、OM、OP、ON表示）  
某实验小组在进行“验证动量守恒定律”的实验．入射球与被碰球半径相同．①实验装置如1图所示．先不放B球，使A球斜槽上某一固定点C由静止滚下，落到位于水平地面的记录纸上留下痕迹．再把B球静置于水平槽前端边缘处，上A球仍从C处静止滚下，A球和B球碰撞后分别落在记录纸上留下各自落点的痕迹．记录纸上的O点是垂锤所指的位置，M、P、N分别为落点的痕迹．未放B球时，A球落地点时记录纸上的
P
P
点．
②释放多次后，取各落点位置的平均值，测得各落点痕迹到O点的距离：PM=13.10cm，OP=21.90cm，ON=26.04cm．用天平称得入射小球A的质量m1=16.8g，被碰小球B的质量m2=5.6g，若将小球质量与水平位移的乘积作为“动量”，请将下面的数据处理表格填写完整：
OP/m OM/m ON/m 碰前总动量p/kg?m 碰后总劝量p′/kg?m 相对误差|
p′-p
p
|×100%
0.2190 0.1310 0.2604 3.68×10-3
3.66×10-3
3.66×10-3
0.54%
0.54%
根据上面表格中的数据处理数据，你认为能得到的结论是：
在实验误差允许范围内，可认为系统在碰前的动量和碰后的动量是相等的．
在实验误差允许范围内，可认为系统在碰前的动量和碰后的动量是相等的．
．
③实验中可以将表达式m1v1=m1v1′+m2v 2′转化为m1s2=m1 s1′+m2s2′来进行验证，其中s1、s1′、s2、
s2′为小球平抛的水平位移．可以进行这种转化的依据是
D
D
．（请选择一个最合适的答案）
A．小球飞出后的加速度相同
B．小球飞出后，水平方向的速度相同
C．小球在空中水平方向都做匀速直线运动，水平位移与时间成正比
D．小球在空中水平方向都做匀速直线运动，又因为从同一高度平扫，运动时间相同，所以水平位移与初速度成正比
④完成实验后，实验小组对上述装置进行了如图2所示的改变：（I）在木板表面先后钉上白纸和复印纸，并将木板竖直立于靠近槽口处，使小球A从斜槽轨道上某固定点C由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球A从原固定点C由静止释放，撞到木板上得到痕迹P；（III）把半径相同的小球B静止放在斜槽轨道水平段的最右端，让小球A仍从原固定点由静止开始滚下，与小球B相碰后，两球撞在木板上得到痕迹M和N；（IV）用刻度尺测量纸上O点到M、P、N三点的距离分别为y1，y2，y3．请你与出用直接测量的物理量来验证两球碰撞过程中动量守恒的表达式：
m1
1
y
 
2
=m1
1
y1
+m2
1
y3
m1
1
y
 
2
=m1
1
y1
+m2
1
y3
．（小球A、B的质量分别为m1、m2）
（Ⅰ）学校科技活动小组的同学们准备自己动手粗略测定铁块与长木板之间的动摩擦因数，已有的器材：长木板、小铁块、米尺和刻度尺．他们同时从实验室借来一个电火花打点计时器，设计了如下实验：
a．用米尺测量长木板总长度l，将打点计时器固定在长木板上．然后将长木板靠在竖直墙壁固定（如图1），并测量长木板顶端B相对于水平地面的高度h和长木板底端A与墙角C之间的距离s；
b．将小铁块连上纸带，接通打点计时器后释放，得到的纸带如下图，A、B、C、D、E是纸带上连续的5个点．
现用刻度尺直接测出AC、CE的距离分别为：x1、x2；已知交流电的频率为f，重力加速度为g．由此可求得铁块的加速度a=
 
；根据牛顿第二定律，可求得动摩擦因数μ=
 
（用f、g和测得物理量的字母表示）．
（Ⅱ）某同学用下图的装置做“验证动量守恒定律”的实验，操作步骤如下：
（1）先将斜槽轨道的末端调整水平，在一块平木板表面先后钉上白纸和复写纸，并将该木板竖立于靠近槽口处，使小球a从斜槽轨道上某固定点处由静止开始滚下，撞到木板在记录纸上留下压痕O．
（2）将木板向右平移适当距离，再使小球a从原固定点由静止释放，撞到木板在记录纸上留下压痕B．
（3）把半径相同的小球b静止放在斜槽轨道水平段的右边缘，让小球a仍从原固定点由静止开始滚下，与b球相碰后，两球撞在木板上，并在记录纸上留下压痕A和C．
①本实验必须测量的物理量是
 
．（填序号字母，要求验证方法简洁可行）
A．小球a、b的质量ma、mb
B．小球a、b的半径r
C．斜槽轨道末端到木板的水平距离 x
D．球a的固定释放点到斜槽轨道末端的高度差h
E．记录纸上O点到A、B、C的距离y1、y2、y3
②放上被碰小球，两球相碰后，小球a在图中的压痕点为
 

③若两球碰撞动量守恒，则应满足的表达式为
 
（用①中测量的量表示）
④若两球发生的是弹性碰撞，则还应满足的表达式为：
 
．精英家教网
用半径相同的小球1和小球2的碰撞验证动量守恒定律，实验装置如图甲所示，斜槽与水平槽圆滑连接．安装好实验装置，在地上铺一张白纸，白纸上铺放复写纸，记下重锤线所指的位置O．实验步骤如下：
精英家教网
步骤1：不放小球2，让小球1从斜槽上A点由静止滚下，并落在地面上．重复多次，用尽可能小的圆，把小球的所有落点圈在里面，其圆心就是小球落点的平均位置；
步骤2：把小球2放在斜槽前端边缘位置B，让小球1从A点由静止滚下，使它们碰撞．重复多次，并使用与步骤1同样的方法分别标出碰撞后两小球落点的平均位置；
步骤3：用刻度尺分别测量三个落地点的平均位置M、P、N离O点的距离，即线段OM、OP、ON的长度．
（1）实验中，直接测定小球碰撞前后的速度是不容易的．但是，可以通过测量
 
（填选项前的符号），间接地解决这个问题．
A．小球开始释放高度h
B．小球抛出点距地面的高度H
C．小球做平抛运动的射程
（2）本实验除需测量线段OM、OP、ON的长度外，还需要测量的物理量有
 
．
A．A、B两点间的高度差h1          B．B点离地面的高度h2
C．小球1和小球2的质量m1、m2      D．小球1和小球2的半径r
（3）经测定，m1=45.0g，m2=7.5g，小球落地点的平均位置距O点的距离如图乙所示．有同学认为，在上述实验中仅更换两个小球的材质，其它条件不变，可以使被碰小球做平抛运动的射程增大．请你用已知的数据，分析和计算出被碰小球m2平抛运动射程ON的最大值为
 
cm．
（4）完成上述实验后，某实验小组对上述装置进行了改造，如图所示．在水平槽末端与水平地面间放置了一个斜面，斜面的顶点与水平槽等高且无缝连接．使小球1仍从斜槽上A点由静止滚下，重复实验步骤1和2的操作，得到两球落在斜面上的平均落点M′、P′、N′．用刻度尺测量斜面顶点到M′、P′、N′三点的距离分别为l1、l2、l3．则验证两球碰撞过程中动量守恒的表达式为
 
（用所测物理量的字母表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网