��Ŀ����
����ѧУ�Ƽ��С���ͬѧ�����Լ����ִ��Բⶨ�����볤ľ��֮��Ķ�Ħ�����������е����ģ���ľ�塢С���顢�׳ߺͿ̶ȳߣ�����ͬʱ��ʵ���ҽ���һ�������ʱ�������������ʵ�飺
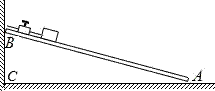
a�����׳߲�����ľ���ܳ���l��������ʱ���̶��ڳ�ľ���ϣ�Ȼ��ľ�忿����ֱǽ�ڹ̶�����ͼ1������������ľ�嶥��B�����ˮƽ����ĸ߶�h�ͳ�ľ���A��ǽ��C֮��ľ���s��
b����С��������ֽ������ͨ����ʱ�����ͷţ��õ���ֽ������ͼ��A��B��C��D��E��ֽ����������5���㣮
���ÿ̶ȳ�ֱ�Ӳ��AC��CE�ľ���ֱ�Ϊ��x1��x2����֪�������Ƶ��Ϊf���������ٶ�Ϊg���ɴ˿��������ļ��ٶ�a= ������ţ�ٵڶ����ɣ�����ö�Ħ��������= ����f��g�Ͳ������������ĸ��ʾ����
����ijͬѧ����ͼ��װ��������֤�����غ㶨�ɡ���ʵ�飬�����������£�
��1���Ƚ�б�۹����ĩ�˵���ˮƽ����һ��ƽľ������Ⱥ��ϰ�ֽ��дֽ��������ľ�������ڿ����ۿڴ���ʹС��a��б�۹����ij�̶��㴦�ɾ�ֹ��ʼ���£�ײ��ľ���ڼ�¼ֽ������ѹ��O��
��2����ľ������ƽ���ʵ����룬��ʹС��a��ԭ�̶����ɾ�ֹ�ͷţ�ײ��ľ���ڼ�¼ֽ������ѹ��B��
��3���Ѱ뾶��ͬ��С��b��ֹ����б�۹��ˮƽ�ε��ұ�Ե����С��a�Դ�ԭ�̶����ɾ�ֹ��ʼ���£���b������������ײ��ľ���ϣ����ڼ�¼ֽ������ѹ��A��C��
�ٱ�ʵ������������������ �����������ĸ��Ҫ����֤���������У�
A����a��b������ma��mb
B��С��a��b�İ뾶r
C��б�۹��ĩ�˵�ľ���ˮƽ���� x
D����a�Ĺ̶��ͷŵ㵽б�۹��ĩ�˵ĸ߶Ȳ�h
E����¼ֽ��O�㵽A��B��C�ľ���y1��y2��y3
�ڷ��ϱ���С������������С��a��ͼ�е�ѹ�۵�Ϊ
����������ײ�����غ㣬��Ӧ����ı���ʽΪ ���â��в���������ʾ��
�������������ǵ�����ײ����Ӧ����ı���ʽΪ�� ��
a�����׳߲�����ľ���ܳ���l��������ʱ���̶��ڳ�ľ���ϣ�Ȼ��ľ�忿����ֱǽ�ڹ̶�����ͼ1������������ľ�嶥��B�����ˮƽ����ĸ߶�h�ͳ�ľ���A��ǽ��C֮��ľ���s��
b����С��������ֽ������ͨ����ʱ�����ͷţ��õ���ֽ������ͼ��A��B��C��D��E��ֽ����������5���㣮
���ÿ̶ȳ�ֱ�Ӳ��AC��CE�ľ���ֱ�Ϊ��x1��x2����֪�������Ƶ��Ϊf���������ٶ�Ϊg���ɴ˿��������ļ��ٶ�a=
����ijͬѧ����ͼ��װ��������֤�����غ㶨�ɡ���ʵ�飬�����������£�
��1���Ƚ�б�۹����ĩ�˵���ˮƽ����һ��ƽľ������Ⱥ��ϰ�ֽ��дֽ��������ľ�������ڿ����ۿڴ���ʹС��a��б�۹����ij�̶��㴦�ɾ�ֹ��ʼ���£�ײ��ľ���ڼ�¼ֽ������ѹ��O��
��2����ľ������ƽ���ʵ����룬��ʹС��a��ԭ�̶����ɾ�ֹ�ͷţ�ײ��ľ���ڼ�¼ֽ������ѹ��B��
��3���Ѱ뾶��ͬ��С��b��ֹ����б�۹��ˮƽ�ε��ұ�Ե����С��a�Դ�ԭ�̶����ɾ�ֹ��ʼ���£���b������������ײ��ľ���ϣ����ڼ�¼ֽ������ѹ��A��C��
�ٱ�ʵ������������������
A����a��b������ma��mb
B��С��a��b�İ뾶r
C��б�۹��ĩ�˵�ľ���ˮƽ���� x
D����a�Ĺ̶��ͷŵ㵽б�۹��ĩ�˵ĸ߶Ȳ�h
E����¼ֽ��O�㵽A��B��C�ľ���y1��y2��y3
�ڷ��ϱ���С������������С��a��ͼ�е�ѹ�۵�Ϊ
����������ײ�����غ㣬��Ӧ����ı���ʽΪ
�������������ǵ�����ײ����Ӧ����ı���ʽΪ��

������������ֽ���������ȱ����˶������ۣ���x=aT2�������С����ļ��ٶ�a������ţ�ٵڶ����ɺ���ѧ֪ʶ������ö�Ħ�������̣�
����a��b�����뿪б�۹��ĩ�˺���ƽ���˶�������ˮƽλ����ȣ�����x������x=v0t��t=
�����ɵõ���ײ��������ٶȱ���ʽ����������ײ�����غ㣬Ӧ����ı���ʽΪmava=mava��+mbvb�䣬���ɵõ�Ӧ����ı���ʽ������ȷ����Ҫ���������������������ǵ�����ײ������Ķ���Ҳ�غ㣬д������ʽ��
����a��b�����뿪б�۹��ĩ�˺���ƽ���˶�������ˮƽλ����ȣ�����x������x=v0t��t=
|
����⣺����AC���CE���ʱ������Ϊ T=
С�������ȼ����˶������ݡ�x=aT2�ã�x2-x1=aT2=a(
)2
��ã�a=
�賤ľ������Ϊ����
�����飬����ţ�ٵڶ����ɵã�mgsin��-��mgcos��=ma
������ѧ֪ʶ�ã�sin��=
��cos��=
����������ʽ��ã���=
-
������a�������¾���б�۹��ĩ�˵��ٶ�Ϊva��������ײ��a��b���ٶȷֱ�Ϊva���vb�䣮
��������ײ�����غ㣬��mava=mava��+mbvb�䣻
����ƽ���˶����ɵã�va=
=x
��va��=x
��vb��=x
��
�����ã�Ӧ����ı���ʽΪ��
=
+
��
���Կ�֪��
�ٱ�ʵ������������������С��a��b������ma��mb����¼ֽ��O�㵽A��B��C�ľ���y1��y2��y3����AE��ȷ��
��ѡ��AE��
�ڷ��ϱ���С������������С��aƽ���˶����ٶȼ�С���˶�ʱ��䳤������y=
gt2֪����ֱ�½��ĸ߶�����������ͼ�е�ѹ�۵�Ϊ C��
�����Ͽ�֪����������ײ�����غ㣬��Ӧ����ı���ʽΪ��
=
+
��
�������������ǵ�����ײ������Ҳ�غ㣬��
ma
=
ma
+
mb
��va=x
��va��=x
��vb��=x
����ã�
=
+
��
�ʴ�Ϊ����
��
-
��
��A��E����C����
=
+
����
=
+
��
| 2 |
| f |
С�������ȼ����˶������ݡ�x=aT2�ã�x2-x1=aT2=a(
| 2 |
| f |
��ã�a=
| (x2-x1)f2 |
| 4 |
�賤ľ������Ϊ����
�����飬����ţ�ٵڶ����ɵã�mgsin��-��mgcos��=ma
������ѧ֪ʶ�ã�sin��=
| h | ||
|
| s | ||
|
����������ʽ��ã���=
| h |
| s |
(x2-x1)f2
| ||
| 4gs |
������a�������¾���б�۹��ĩ�˵��ٶ�Ϊva��������ײ��a��b���ٶȷֱ�Ϊva���vb�䣮
��������ײ�����غ㣬��mava=mava��+mbvb�䣻
����ƽ���˶����ɵã�va=
| x |
| t |
|
|
|
�����ã�Ӧ����ı���ʽΪ��
| ma | ||
|
| ma | ||
|
| mb | ||
|
���Կ�֪��
�ٱ�ʵ������������������С��a��b������ma��mb����¼ֽ��O�㵽A��B��C�ľ���y1��y2��y3����AE��ȷ��
��ѡ��AE��
�ڷ��ϱ���С������������С��aƽ���˶����ٶȼ�С���˶�ʱ��䳤������y=
| 1 |
| 2 |
�����Ͽ�֪����������ײ�����غ㣬��Ӧ����ı���ʽΪ��
| ma | ||
|
| ma | ||
|
| mb | ||
|
�������������ǵ�����ײ������Ҳ�غ㣬��
| 1 |
| 2 |
| v | 2 a |
| 1 |
| 2 |
| v | ��2 a |
| 1 |
| 2 |
| v | ��2 b |
��va=x
|
|
|
| ma |
| y2 |
| ma |
| y3 |
| mb |
| y1 |
�ʴ�Ϊ����
| (x2-x1)f2 |
| 4 |
| h |
| s |
(x2-x1)f2
| ||
| 4gs |
��A��E����C����
| ma | ||
|
| ma | ||
|
| mb | ||
|
| ma |
| y2 |
| ma |
| y3 |
| mb |
| y1 |
�����������1��Ҫ����ֽ��������ԭ������x=aT2�ͻ������ٶȵ�ԭ����ţ�ٵڶ����ɣ���ľ�����Dz����������������ѧ֪ʶ��ɲ���h��s���������ľ����ǵ����Һ����ң�
��2��ؼ�����ƽ���˶���֪ʶ�õ�ƽ���˶��ij��ٶȣ�֪����Ҫ��֤�ķ��̣�
��2��ؼ�����ƽ���˶���֪ʶ�õ�ƽ���˶��ij��ٶȣ�֪����Ҫ��֤�ķ��̣�

��ϰ��ϵ�д�
�����Ŀ
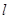 ��������ʱ���̶��ڳ�ľ���ϡ�Ȼ��ľ�忿����ֱǽ�ڹ̶�����ͼ������������ľ�嶥��B�����ˮƽ����ĸ߶�
��������ʱ���̶��ڳ�ľ���ϡ�Ȼ��ľ�忿����ֱǽ�ڹ̶�����ͼ������������ľ�嶥��B�����ˮƽ����ĸ߶�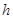 �ͳ�ľ���A��ǽ��C֮��ľ���
�ͳ�ľ���A��ǽ��C֮��ľ���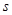 ��
��
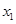 ��
�� ����֪�������Ƶ��Ϊ
����֪�������Ƶ��Ϊ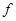 ���������ٶ�Ϊ
���������ٶ�Ϊ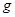 .�ɴ˿��������ļ��ٶ�
.�ɴ˿��������ļ��ٶ�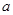 ��
������ţ�ٵڶ����ɣ�����ö�Ħ������
��
������ţ�ٵڶ����ɣ�����ö�Ħ������ ��
(��
��
(��