Question

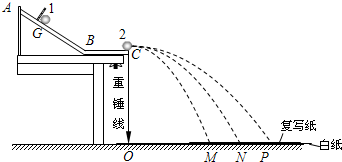某同学用如图所示的装置，利用两个大小相同的小球做对心碰撞来验证动量守恒定律，图中AB是斜槽，BC是水平槽，它们连接平滑，O点为重锤线所指的位置．实验时先不放置被碰球2，让球1从斜槽上的某一固定位置G由静止开始滚下，落到位于水平地面的记录纸上，留下痕迹，重复10次．然后将球2置于水平槽末端，让球1仍从位置G由静止滚下，和球2碰撞．碰后两球分别在记录纸上留下各自的痕迹，重复10次．实验得到小球的落点的平均位置分别为 M、N、P．
（1）在此实验中，球1的质量为m₁，球2的质量为m₂，需满足m₁

大于

 m₂（选填“大于”、“小于”或“等于”）．
（2）被碰球2飞行的水平距离由图中线段

.

OP

表示．
（3）若实验结果满足m1?

.

ON

=

m₁?

.

OM

+m₂?

.

OP

，就可以验证碰撞过程中动量守恒．

Answer 1

分析：（1）为了保证碰撞前后使入射小球的速度方向不变，故必须使入射小球的质量大于被碰小球的质量．
（2）小球1和小球2相撞后，小球2的速度增大，小球1的速度减小，都做平抛运动，由平抛运动规律不难判断出；
（3）先根据平抛运动的特点判断碰撞前后两个小球的落地点，再求出碰撞前后两个小球的速度，根据动量的公式列出表达式，代入数据看碰撞前后的动量是否相等．

解答：解：（1）在小球碰撞过程中水平方向动量守恒定律故有m₁v₀=m₁v₁+m₂v₂
在碰撞过程中动能守恒故有

1

2

m₁v₀²=

1

2

m₁v₁²+

1

2

m₂v₂²
解得v₁=

m1-m2

m1+m2

v0
要碰后入射小球的速度v₁＞0，即m₁-m₂＞0，
故答案为：大于．
（2）1球和2球相撞后，2球的速度增大，1球的速度减小，都做平抛运动，竖直高度相同，所以所以碰撞后2球的落地点是P点，所以被碰球2飞行的水平距离由图中线段

.

OP

表示；
（3）N为碰前入射小球落点的位置，M为碰后入射小球的位置，P为碰后被碰小球的位置，
碰撞前入射小球的速度v1=

. ON

2h g

碰撞后入射小球的速度
v2=

. OM

2h g

碰撞后被碰小球的速度v3=

. OP

2h g

若m₁v₁=m₂v₃+m₁v₂则表明通过该实验验证了两球碰撞过程中动量守恒，
带入数据得：m₁

.

ON

=m₁

.

OM

+m₂

.

OP

故答案为：大于；

.

OP

；m₁?

.

OM

+m₂?

.

OP

点评：本题是运用等效思维方法，平抛时间相等，用水平位移代替初速度，这样将不便验证的方程变成容易验证．