题目内容
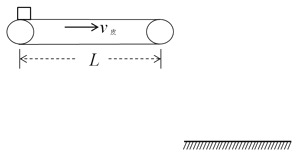
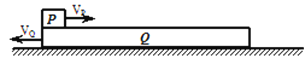
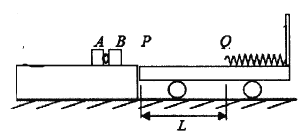
【题目】如图所示，固定的光滑平台上静止着两个滑块A、B，mA＝0.lkg，mB＝0.2kg，两滑块间夹有少量炸药，平台右侧有一带挡板的小车，静止在光滑的水平地面上。小车质量为M＝0.3kg，车面与平台的台面等高，小车的上表面的右侧固定一根轻弹簧，弹簧的自由端在Q 点，小车的上表面左端点P与Q点之间是粗糙的，P、Q间距L＝0.75m，滑块B与PQ之间表面的动摩擦因数为
＝0.2， Q点右侧表面是光滑的。点燃炸药后，A、B分离瞬间A滑块获得向左的速度vA＝6m/s，而滑块B则冲向小车。两滑块都可以看作质点，炸药的质量忽略不计，爆炸的时间极短，爆炸后两个物块的速度方向在同一水平直线上，且g＝l0m/s2。求：
(1)滑块B滑上小车后的运动过程中弹簧的最大弹性势能；
(2)滑块B运动到何处小车速度最大? 并求出小车运动过程中的最大速度。
【答案】(1)EP＝0.24J (2)滑块B压缩弹簧后返回Q点时小车速度最大 小车最大速度为2m/s
【解析】
（1）炸药爆炸过程系统动量守恒，应用动量守恒定律求出爆炸后B的速度，弹簧压缩到最短过程弹性势能最大，应用动量守恒定律与能量守恒定律分析答题．
（2）滑块B返回Q点时小车速度最大，对B与小车组成的系统，应用动量守恒定律与能量守恒定律可以求出小车的最大速度．
（1）爆炸过程系统动量守恒，以向左为正方向，由动量守恒定律得：mAvA-mBvB=0，
解得：vB=3m/s，
弹簧压缩到最短时弹簧的弹性势能最大，B与小车组成的系统动量守恒，以向右为正方向，由动量守恒定律得：mBvB=（M+mB）v，
由能量守恒定律得：
mBvB2=（M+mB）v2+μmBgL+EP，
解得：EP=0.24J；
（2）滑块B压缩弹簧后返回Q点时小车的速度最大，系统动量守恒，
以向右为正方向由动量守恒定律得：mBvB=mBv1+Mv2，
由能量守恒定律得：mBvB2=mBv12+Mv22+μmBgL，
解得：v1=0，v2=2m/s，（v1=2.4m/s，v2=0.4m/s B的速度大于车的速度，不符合实际，舍去）；
