��Ŀ����
����Ŀ����ͼ��ʾ��������ת����Բ���ϣ��ذ뾶���������ϸ��������������Ϊm��A��B����С��飬A������r1��20 cm��B������r2��30 cm��A��B�����������õ����Ħ����Ϊ��������0.4������
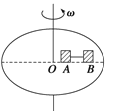
(1)��ϸ����û��������Բ��ת���Ľ��ٶȦ�Ӧ����ʲô������
(2)��ʹA��B������䲻������Ի���������ת���������ٶȶ��
(3)��Բ��ת�ٴﵽA��B�պò�����ʱ���ն�ϸ������A��B�������˶���(gȡ10 m/s2)
���𰸡�(1) ���ءܦ�0��3.6 rad/sʱ��ϸ���ϲ�����������(2) 4.0 rad/s.
��������(1)�����B����������FB��Ffmʱ��ϸ��������Ϊ�㣮���Ž��ٶȵ�����FB��Ffmʱ����kmg��m��![]() r2��
r2��
�æ�0��![]() ��
��![]() ��
��![]() ��3��6 rad/s.
��3��6 rad/s.
���ءܦ�0��3.6 rad/sʱ��ϸ���ϲ�����������
(2)��A��B���ܾ�Ħ�������ﵽ���Ħ����ʱ��Բ�̵Ľ��ٶȴﵽ���ֵ��m��������mʱ��A��B�����Բ�̻�����(��ϸ��������ΪT.)
��A��kmg��T��m��m2��r1��
��B��kmg��T��m��m2��r2��
��æ�m��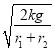 ��
��![]()
��4.0 rad/s.
(3)�ն�ϸ��ʱ��A��Բ���˶�����������FA��m��m2r1��3.2 N�����Ħ����Ϊ4 N��A��������һ��ת����B��ʱ����������ΪFB��m��m2r2��4.8 N�������������Ħ����4 N�����B���彫��һ�������˶�����Բ��Խ��ԽԶ��
��������Բ���˶������������ؾ�����ĺ����ṩ�������Ħ�����ṩ���ڶ����зֱ�����С��Ϊ�о��������ӵ������;�Ħ�����ĺ����ṩ��������ʽ���