题目内容
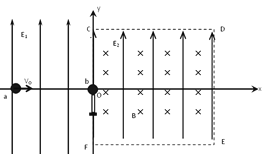
【题目】如图所示的xoy坐标系中，y轴右侧空间存在范围足够大的匀强磁场，磁感应强度大小为B，方向垂直于xoy平面向里。P点的坐标为(-6L，0)，Q1、Q2两点的坐标分别为(0，3L)，(0，-3L).坐标为(-L，0)处的C点固定一平行于y轴放置一足够长的绝缘弹性挡板，带电粒子与弹性绝缘挡板碰撞前后，沿y方向分速度不变，沿x方向分速度反向，大小不变.带负电的粒子质量为m，电量为q，不计粒子所受重力.若粒子在P点沿PQ1方向进入磁场，经磁场运动后，求：
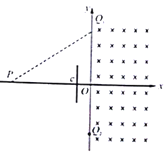
(1)不与挡板碰撞并能回到P点的粒子初速度大小；
(2)只与挡板碰撞一次并能回到P点的粒子初速度大小；
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为多少？
【答案】（1）
（2）
（3）
；2.5L
【解析】
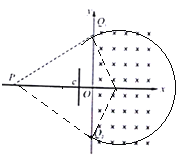
（1）当粒子不与挡板碰撞时，作出粒子运动的轨迹图，结合几何关系求出粒子在磁场中运动的轨道半径，根据半径公式求出粒子的速度。
（2）当粒子与挡板碰撞一次时，作出粒子运动的轨迹图，结合几何关系求出粒子在磁场中运动的轨道半径，根据半径公式求出粒子的速度。
（3）粒子与挡板碰撞三次并能回到P点，作出轨迹图，结合几何关系，运用半径公式进行求解。
（1）粒子不与挡板碰撞并能回到P点，则由几何关系可知
解得
根据
解得
（2）粒子与挡板只碰撞一次，粒子运动的轨迹如图所示：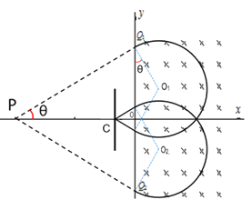
粒子运动的轨道半径为R2，碰撞前后出入磁场两点之间的距离为L，则：
根据几何关系可得：4R2cosθ-L=6L，其中：
解得：
①
根据半径公式：
②
联立①②式可得：
（3）若与挡板碰撞三次，如图三所示，设挡板的长度L0，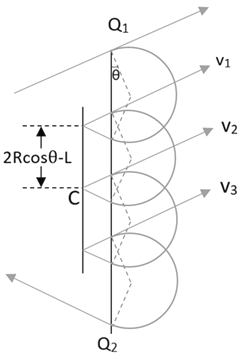
根据几何关系可得：3（2R3cosθ-L）+2R3cosθ=6L
解得：R3=
根据半径公式：
可得：
联立式子可得：挡板的长度的最小值L0=2（2Rcosθ-L）=2.5L
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
