题目内容
(选修3-4)
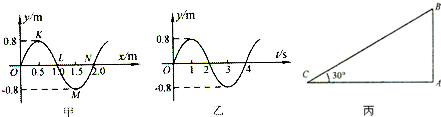
(1)如图1所示,一列简谐横波沿+x方向传播.已知在t=0时,波传播到x轴上的B质点,在它左边的A质点位于负最大位移处;在t=0.6s时,质点A第二次出现在正的最大位移处.
①这列简谐波的周期是 s,波速是 m/s.
②t=0.6s时,质点D已运动的路程是 m.
(2)在水面上放置一个足够大的遮光板,板上有一个半径为r的圆孔,圆心的正上方h 处放一个点光源S,在水面下深H处的底部形成半径为R的圆形光亮区域(图2中未画出).测得r=8cm,h=6cm,H=24cm,R=26cm,求水的折射率.

(1)如图1所示,一列简谐横波沿+x方向传播.已知在t=0时,波传播到x轴上的B质点,在它左边的A质点位于负最大位移处;在t=0.6s时,质点A第二次出现在正的最大位移处.
①这列简谐波的周期是
②t=0.6s时,质点D已运动的路程是
(2)在水面上放置一个足够大的遮光板,板上有一个半径为r的圆孔,圆心的正上方h 处放一个点光源S,在水面下深H处的底部形成半径为R的圆形光亮区域(图2中未画出).测得r=8cm,h=6cm,H=24cm,R=26cm,求水的折射率.

分析:(1)根据A质点位置的变化,可以得出该波的周期,结合波长即可求得波速;由图分析D点的振动时间,从而可知D所经过的路程.
(2)根据几何关系,分别求出入射角的正弦值和折射角的正弦值,即可得出水的折射率.
(2)根据几何关系,分别求出入射角的正弦值和折射角的正弦值,即可得出水的折射率.
解答:解:(1)①A质点从负的最大位移处到第二次到达正的最大位移处所经历的时间为一个半周期,即为:t=
T
得:T=0.4s
由图可知这列波的波长为λ=2m,由公式v=
得:
v=
=5m/s
②质点BD之间相距2m,为一个波长,所以波从B传到D需要一个周期,故可知0.6s内D点只振动了半个周期,所以D点经过的路程为:
s=
×4A=10cm=0.1m
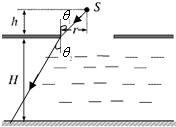 (2)根据光路图(如图所示),可知sinθ1=
(2)根据光路图(如图所示),可知sinθ1=
=
=0.8
sinθ2=
=
=0.6
由折射定律有:n=
得:n=
故答案为:(1)①0.4,5;②0.1
(2)水的折射率为
| 3 |
| 2 |
得:T=0.4s
由图可知这列波的波长为λ=2m,由公式v=
| λ |
| T |
v=
| 2 |
| 0.4 |
②质点BD之间相距2m,为一个波长,所以波从B传到D需要一个周期,故可知0.6s内D点只振动了半个周期,所以D点经过的路程为:
s=
| 1 |
| 2 |
 (2)根据光路图(如图所示),可知sinθ1=
(2)根据光路图(如图所示),可知sinθ1=| r | ||
|
| 8 | ||
|
sinθ2=
| R-r | ||
|
| 18 | ||
|
由折射定律有:n=
| sinθ1 |
| sinθ2 |
得:n=
| 4 |
| 3 |
故答案为:(1)①0.4,5;②0.1
(2)水的折射率为
| 4 |
| 3 |
点评:第一小题考察了波的传播,要知道波速、波长及周期(频率)的关系,即:v=
=λf,波传播过程中,某质点振动所经过的路程为振动时间和周期的比值(往往是四分之一周期的倍数)与4倍振幅的成绩.
第二小题考察了求折射率的问题,关键是利用几何关系找出入射角和折射角,并分别求出它们的正弦值.要特别注意光线从光密介质射向光疏介质的情况.
| λ |
| T |
第二小题考察了求折射率的问题,关键是利用几何关系找出入射角和折射角,并分别求出它们的正弦值.要特别注意光线从光密介质射向光疏介质的情况.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
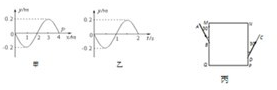 【物理-选修3-4】
【物理-选修3-4】 (1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则
(1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则 (2011?吉安模拟)〔物理--选修3-4〕
(2011?吉安模拟)〔物理--选修3-4〕 砖的折射率为n(n<2),不考虑光在OA、OB面的反射.问:
砖的折射率为n(n<2),不考虑光在OA、OB面的反射.问: