题目内容
物理-选修3-4模块
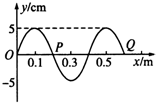
 (1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则
(1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则
A.波的周期为2.4s
B.在t=0.9s时,P点沿y轴正方向运动
C.经过0.4s,P点经过的路程为4m
D.在t=0.5s时,Q点到达波峰位置
(2)在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图2所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃上表面的垂直距离L应是多少?
 (1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则
(1)图1所示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6s时的波形图,波的周期T>0.6s,则D
D
A.波的周期为2.4s
B.在t=0.9s时,P点沿y轴正方向运动
C.经过0.4s,P点经过的路程为4m
D.在t=0.5s时,Q点到达波峰位置
(2)在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图2所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃上表面的垂直距离L应是多少?
分析:(1)应用平移法求出波的波长和周期;根据波的传播方向确定质点的振动方向;在一个周期内质点完成一个全振动,运动路程为4A;后一个质点重复前一个质点的振动,故t=0.5s时,Q点振动情况和t=0时距离坐标原点x=x0+vt=10m处的质点的振动情况相同.
(2)根据数学知识分别用L表示光在空气中走过的距离和在玻璃中走过的距离.光在玻璃传播的速度,由折射定律求出折射角的正弦值.根据题意:光从光源到玻璃板上表面的传播时间与光在玻璃中传播的时间相等,列式求出L.
(2)根据数学知识分别用L表示光在空气中走过的距离和在玻璃中走过的距离.光在玻璃传播的速度,由折射定律求出折射角的正弦值.根据题意:光从光源到玻璃板上表面的传播时间与光在玻璃中传播的时间相等,列式求出L.
解答:解:A、根据题意应用平移法可知由实线得到虚线需要将图象沿x轴负方向平移(n+
)λ,其中n=0、1、2、3、4…,
故由实线传播到虚线这种状态需要(n+
)T,即(n+
)T=0.6s,解得T=
,其中n=0、1、2、3、4…,当n=0时,解得T=0.8s,当n=1时,解得T=0.34s,
又T>0.6s,故最大周期为0.8s,故A错;
B、由于波沿x轴负方向传播,故t=0时p点沿y轴负方向运动,故t=0.8s时p点沿y轴负方向运动,而周期T=0.8s,故0.9s时P点沿y轴负方向运动.故B错误.
C、在一个周期内p点完成一个全振动,即其运动路程为4A,而0.4s=
T,故p点的运动路程为2A=0.4m,C错;
D、由题意可知波长λ=8m,则变速v=
=10m/s,在t=0时Q点的横坐标为5m,由于波沿y轴负方向运动,故在t=0.5s的时间内波沿x轴负方向传播的距离为x=vt=10×0.5=5m,故在t=0.5s时,Q点振动情况和t=0时距离坐标原点10m处的质点的振动情况相同,而t=0时距离坐标原点10m处的质点在波峰,在t=0.5s时,Q点到达波峰位置.故D正确.
故选D.
(2)设折射角为r,SA=
光线从S到玻璃板上表面的传播时间为:t1=
光在玻璃板中的传播距离:S=
光在玻璃板中的传播时间为:t2=
由题意知:
=
由折射定律sinθ=nsinr
联立解得:l=
d
| 1 |
| 4 |
故由实线传播到虚线这种状态需要(n+
| 3 |
| 4 |
| 3 |
| 4 |
| 2.4 |
| 4n+3 |
又T>0.6s,故最大周期为0.8s,故A错;
B、由于波沿x轴负方向传播,故t=0时p点沿y轴负方向运动,故t=0.8s时p点沿y轴负方向运动,而周期T=0.8s,故0.9s时P点沿y轴负方向运动.故B错误.
C、在一个周期内p点完成一个全振动,即其运动路程为4A,而0.4s=
| 1 |
| 2 |
D、由题意可知波长λ=8m,则变速v=
| λ |
| T |
故选D.
(2)设折射角为r,SA=
| l |
| cosθ |
光线从S到玻璃板上表面的传播时间为:t1=
| l |
| Ccosθ |
光在玻璃板中的传播距离:S=
| d |
| cosr |
光在玻璃板中的传播时间为:t2=
| nd |
| Ccosr |
由题意知:
| nd |
| cosr |
| l |
| cosθ |
由折射定律sinθ=nsinr
联立解得:l=
| ncosθ | ||||
|
点评:把握“后一个质点重复前一个质点的运动情况”,是解决本题中D的关键;本题是折射定律、及数学知识的综合应用,突破口是光在空气中和玻璃中的时间相等,将此文字语言变成数学表达式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 [物理选修3-4模块]
[物理选修3-4模块]


