题目内容
【题目】静止在水平地面上的两小物块A、B,质量分别为mA=1.0kg,mB=4.0kg;两者之间有一被压缩的微型弹簧(长度不计),其弹性势能为10.0J,A与其右侧的竖直墙壁距离l=1.0m,如图所示。某时刻,将压缩的微型弹簧释放,使A、B瞬间分离,两物块获得的速度之比是vA︰vB=4︰1。释放后,A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为μ=0.20。重力加速度取g=10m/s2。A与墙壁碰撞前后动能不变且碰撞时间不计。求:
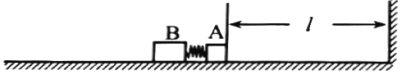
(1)弹簧释放后瞬间A、B速度的大小;
(2)物块A、B中有一个停下来时,A与B之间的距离。
【答案】(1) vA =4m/s,vB=1m/s (2) 0.5m
【解析】
(1)弹簧释放后瞬间,弹性势能转化为A、B动能Ep弹=![]()
vA︰vB=4︰1
联立得vA =4m/s,vB=1m/s
(2)A、B加速度大小相等,a=μg=2m/s2
B速度较小先停下,所用时间t=vB/a=0.5s
B向左位移sB= vB2/2a=0.25m
A该时间内的路程sA=vAt-![]() =1.75m
=1.75m
A与B之间的距离sAB=sB+L-(sA-L)=0.5m

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目