题目内容
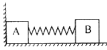
【题目】如图所示，A、B、C三个小物块放置在光滑水平面上，A紧靠墙壁，A、B之间用轻弹簧栓接，它们的质量分别为mA=m，mB=2m，mC=m．现给C一水平向左的初速度v0，C与B发生碰撞并粘在一起。试求：
（1）A离开墙前，弹簧的最大弹性势能；
（2）A离开墙后，弹簧的最大弹性势能；
（3）A离开墙后，C的最小速度。
【答案】（1）
；（1）
；（1）
【解析】
（1）C、B碰撞过程遵守动量守恒，即可列式求出碰后BC共同速度vBC．再运用机械能守恒求解．
（2）在A离开墙壁时，弹簧处于原长，B、C以速度vBC向右运动，之后，A、B、C及弹簧组成的系统机械能守恒，动量也守恒．由于弹簧的作用，A的速度逐渐增大，BC的速度逐渐减小当三者速度相同时，弹性势能再次达到最大值，运用机械能守恒求解；
（3）根据上面的分析可知当弹簧再次恢复原长时，B与C的速度最小，由动量守恒定律和功能关系即可求出；
（1）C、B碰撞过程，选取向左为正方向，根据动量守恒得：
得：
BC一起压缩弹簧到最短的过程，BC和弹簧组成的系统机械能守恒，则弹簧压缩到最短时弹性势能最大，有：
联立以上两式解得，
；
（2）在A离开墙壁时，弹簧处于原长，B、C以速度vBC向右运动，在A离开墙壁后由于弹簧的作用，A的速度逐渐增大，BC的速度逐渐减小，当三者速度相同时，弹簧的伸长量最大，弹性势能再次最大，则选取向右为正方向，根据动量守恒：
，则：
根据机械能守恒有：
；
（3）在A离开墙壁时，弹簧处于原长，B、C以速度vBC向右运动，在A离开墙壁后由于弹簧的作用，A的速度逐渐增大，BC的速度逐渐减小，当弹簧再次恢复原长时，B与C的速度最小，选取向右为正方向，由ABC三物体组成系统动量守恒得：
又：
联立解得：
，方向向右，（另一个解不合题意，舍去）。
