题目内容

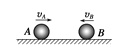
【题目】如图，两滑块A、B在光滑水平面上沿同一直线相向运动，滑块A的质量为m，速度大小为2v0，方向向右，滑块B的质量为2m，速度大小为v0，方向向左，两滑块发生弹性碰撞后的运动状态是(　　)

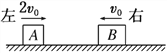
A. A和B都向左运动

B. A和B都向右运动

C. A静止，B向右运动

D. A向左运动，B向右运动

【答案】D

【解析】解：两球碰撞过程动量守恒，以两球组成的系统为研究对象，取水平向右方向为正方向，碰撞前，A、B的速度分别为：vA=2v0、vB=v0．

碰撞前系统总动量：P=mAvA+mBvB=m×2v0+2m×（﹣v0）=0，P=0，

系统总动量为0，系统动量守恒，则碰撞前后系统总动量都是0；

若碰撞为完全非弹性碰撞，则碰撞后二者的速度相等，都是0；

若碰撞不是完全非弹性碰撞，则碰撞后二者的速度方向运动相反．

故D正确，ABC错误．

故选：D．

练习册系列答案
相关题目

【题目】一步行者以6.0 m/s的速度跑去追赶被红灯阻停的公交车，在跑到距汽车25 m处时，绿灯亮了，汽车以1.0 m/s2的加速度匀加速启动前进，则（ ）

A. 人能追上公共汽车，追赶过程中人跑了36 m

B. 人不能追上公共汽车，人、车最近距离为7 m

C. 人能追上公共汽车，追上车前人共跑了43 m

D. 人不能追上公共汽车，且车开动后，人车距离越来越远

【答案】B

【解析】试题分析：开始阶段，人的速度大于汽车的速度，人和车的距离在减小；当人的速度小于汽车的速度时，人和车的增大，当人和车的速度相等时，两者距离最小，设经过时间t两者速度相等， ，此时步行者的位移为，汽车的位移为， ，故不能追上；人车最近距离是。

故选B

考点：追及问题

点评：追和被追的两者的速度相等常是能追上、追不上、二者之间的距离有极值的临界条件． (1)在两个物体的追及过程中，当追者的速度小于被追者的速度时，两者的距离在增大； (2)当追者的速度大于被迫者的速度时，两者的距离在减小；(3)当两者的速度相等时，两者的间距有极值，是最大值还是最小值，视实际情况而定。

【题型】单选题
【结束】
12

【题目】如图所示，两光滑斜面在B处连接，小球从A处由静止释放，经过B、C两点时速度大小分别是3 m/s和4 m/s，AB＝BC.设球经过B点前后速度大小不变，则下列判断正确的是(　　)

A. 球在AB、BC段的加速度大小之比为4∶3

B. 球由A运动到C的过程中平均速率为2.1 m/s

C. 小球在AB、BC段的运动时间之比为7∶4

D. 小球从B运动到C过程中平均速度大小为3.5 m/s

【题目】如油画所示是伽利略研究自由落体运动时的情景，他设计并做了小球在斜面上运动的实验，关于这个实验的下列说法中不符合史实的是

A. 伽利略以实验来检验速度与时间成正比的猜想是否真实

B. 伽利略让小球沿阻力很小的斜面滚下是为了“冲淡”重力的影响

C. 伽利略通过实验发现小球沿斜面滚下的运动是匀加速直线运动

D. 伽利略用实验而不是外推的方法得到斜面倾角增大到90小球仍然会保持匀加速运动

【题目】甲和乙两个物体同地做同向直线运动，他们的位移s随时间t变化的关系图象如图所示，则在0~t1时间内，

A．甲的速度始终比乙的速度大

B．甲的平均速度等于乙的平均速度

C．甲始终在乙的前面，直到t1时刻相遇

D．0~t0时间内，甲在乙的前面，t0~t1时间内，乙在甲的前面

【题目】某同学用图所示装置测量重力加速度，他得到的一条纸带如图所示，，A、B、C是打点计时器连续打下的3个点，但O（速度不为零）、A间还有若干点未标出。该同学按正常的读数要求，用刻度尺测量O到A、B、C各点的距离，并记录在图中。已知电火花计时器的周期为0．02s。

［要求（1）（2）题均保留3位有效数字］

（1）打点计时器打下点B时，物体的速度大小υB=_________m/s；

（2）计算出当地的重力加速度为g=__________m/s2；

（3）当地的重力加速度数值为9．8m/s2，请列出测量值与当地重力加速度的值有差异的一个原因___________。

【题目】如图所示，两个小球A、B在光滑水平地面上相向运动，它们的质量分别为mA＝4 kg，mB＝2 kg，速度分别是vA＝3 m/s(设为正方向)，vB＝－3 m/s.则它们发生正碰后，速度的可能值分别为(　　)

A. vA′＝1 m/s，vB′＝1 m/s

B. vA′＝4 m/s，vB′＝－5 m/s

C. vA′＝2 m/s，vB′＝－1 m/s

D. vA′＝－1 m/s，vB′＝－5 m/s

【题目】、为相距遥远的两颗行星，距各自表面相同高度处各有一颗卫星、做匀速圆周运动，图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a，横坐标表示物体到行星中心的距离r的平方，两条曲线分别表示、周围的a与的反比关系，它们左端点横坐标相同，则( )

A. 、的平均密度相等

B. 的第一宇宙速度比的小

C. 的公转周期比的大

D. 的向心加速度比的大

【题目】在“验证牛顿第二定律”的实验中，采用如图所示的实验装置，小车及车中砝码的质量用M表示，砂和砂桶的质量用m表示，小车的加速度可由小车后拖动的纸带计算出。

(1)实验中，为了使细线对小车的拉力等于小车所受的合外力，先调节长木板一端滑轮的高度，使细线与长木板平行。接下来还需要进行的一项操作是（_______）

A．将长木板水平放置，让小车连着已经穿过打点计时器的纸带，给打点计时器通电。改变砂桶中砂子的多少，使小车在砂和砂桶的牵引下运动，从打出的纸带判断小车是否做匀速运动

B．将长木板的一端垫起适当的高度，让小车连着已经穿过打点计时器的纸带，撤去砂和砂桶，给打点计时器通电，轻推小车，从打出的纸带判断小车是否做匀速运动

C．将长木板的一端垫起适当的高度，撤去纸带以及砂和砂桶，轻推小车，观察判断小车是否做匀速运动

(2)实验中要进行质量m和M的选取，以下最合理的一组是（_______）

A．M=200g，m=10g、15g、20g、25g、30g、35g、40g

B．M=200g，m=20g、40g、60g、80g、100g、120g

C．M=400g，m=10g、15g、20g、25g、30g、35g、40g

D．M=400g，m=20g、40g、60g、80g、100g、120g

(3)已知打点计时器使用的交流电频率为50Hz，每相邻两个计数点间还有4个点未画出，利用下图给出的数据可求出小车运动的加速度a=______m/s2。(结果保留三位有效数字)

【题目】关于瞬时速度和平均速度的说法，正确的是：

A. 平均速度一定等于初速度与末速度的平均值

B. 极短的时间Δt内的平均速度，就可认为等于Δt内任意时刻的瞬时速度

C. 平均速度为0的物体，一定始终处于静止状态

D. 任意时刻瞬时速度都相等的两个物体，它们的平均速度不一定相等

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网