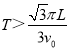��Ŀ����
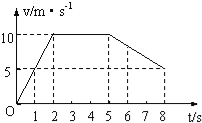
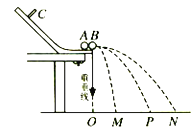
����Ŀ����ͼ(��)��ʾ������������ŵ�ɵ�ƽ�н�����ƽ����x����ã��峤ΪL����������Ϊ2y0����������Ҳ��ΪL�������ڴ�����ͼ(��)��ʾ�����Ա仯�Ĵų����ų������ұ߽���x�ᴹֱ������һ����Ϊm���������Ϊ+q�Ĵ������ӣ���y���ϵ� A�����ٶ�v0��x����������������֮�䣬�ɳ��糡��ӵ�(L��0)����ų�������ʱ�ٶȷ�����x��н�Ϊ30�㣬�����ӽ���ų���ʱ����Ϊ��ʱ�̣��Դ�ֱ��ֽ��������Ϊ�ų���������������x����(2L��0)����x���������30��нǷɳ��ų���������������.

(1)��������������˶�ʱ�糡�����������Ĺ���
(2)���������ĵ��Ʋȷ��A���λ�ã�
(3)д���ų�����Ÿ�Ӧǿ��B0�Ĵ�С���ų��仯����TӦ����ı���ʽ��
���𰸡���1��![]() ��2��
��2��![]() ��
��![]() ��3��
��3��![]() ��n=1��2��3��������
��n=1��2��3��������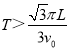
��������
�����������1�������Ӹս���ų�ʱ���ٶ�Ϊv����![]()
�糡�������������Ĺ�Ϊ��![]()
��2�������Ӹս���ų�ʱ����ֱ���ٶ�Ϊv�䣬��
v��=v0tan30��=![]()
ˮƽ����L=v0t
��ֱ����y��![]() v��t
v��t
��ã�![]()
�糡�������������Ĺ���W=qEy
�����ĵ�ѹU=2Ey0
��ã�![]()
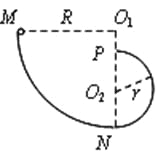
��3���ɶԳ��Կ�֪�����Ӵ�x=2L��ɳ��ų����ٶȴ�С���䣬������x��н�Ϊ��=��30�㣻
�ڴų��仯�İ�������ڣ����ӵ�ƫת��Ϊ2��=60�㣻
�ʴų��仯�İ�������ڣ�������x���ϵ�λ��Ϊ��x=2Rsin30��=R
���ӵ���x=2L�����ٶ���������Ҫ���ǣ�
nR=L ![]() ��n=1��2��3������
��n=1��2��3������
��ţ�ٵڶ����ɣ��У�![]()
��ã�![]() ��n=1��2��3������
��n=1��2��3������
�����ڱ仯�ų��İ��������ǡ��ת��![]() ���ڣ�ͬʱ�ڴų����˶���ʱ���DZ仯�ų�������ڵ�����������ʹ���ӵ���x=2L���������ٶ�����Ҫ��
���ڣ�ͬʱ�ڴų����˶���ʱ���DZ仯�ų�������ڵ�����������ʹ���ӵ���x=2L���������ٶ�����Ҫ��![]() ��
��![]()

��ã� ��n=1��2��3������
��n=1��2��3������
��![]() ��
��