题目内容
【题目】如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为
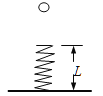
A.(mg-f)(H-L+x) B.mg(H-L+x)-f(H-L)
C.mgH-f(H-L) D.mg(L-x)+f(H-L+x)
【答案】A
【解析】
试题分析:由能量守恒定律知,小球从开始下落到弹簧被压缩到最短的过程中,小球的重力势能转化为弹簧的弹性势能、内能(大小等于阻力做的功)和动能,在压缩到最低时重力所做的功等于克服阻力做功和弹簧最大弹性势能之和,因此有Mg(H-L+x)=f(H-L+x)+EP 解得弹性势能EP为:EP=(mg-f)(H-L+x) 所以A正确,B、C、D错误。

练习册系列答案
相关题目
【题目】下表是某同学为探究弹力和弹簧伸长的关系所测的几组数据:
弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
弹簧的伸长量x/cm | 2.6 | 5.0 | 6.8 | 9.8 | 12.4 |
(1)请你在图中的坐标线上作出F-x图象.

(2)写出曲线所代表的函数.(x用m作单位)
(3)解释函数表达式中常数的物理意义.