题目内容

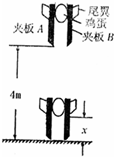
在某中学举办的头脑奥林匹克竞赛中，有一个叫做“保护鸡蛋”的竞赛项目，要求制作一个装置，让鸡蛋从两层楼的高度落到地面且不被摔坏，如果没有保护，鸡蛋最多只能从0.1m的高度落到地面而不被摔坏；有一位同学设计了如图所示的一个装置来保护鸡蛋，用A、B两块较粗糙的夹板夹住鸡蛋，A夹板和B夹板与鸡蛋之间的摩擦力都为鸡蛋重力的5倍，现将该装置从距地面4m的高处落下，装置着地时间短且保持竖直不被弹起，鸡蛋落地后，两板对鸡蛋没有摩擦力．取g=10m/s2，不考虑空气阻力，求：
（1）如果没有保护，鸡蛋直接撞击地面而不被摔坏，其速度最大不能超过多少？（结果用根号表示）
（2）如果使用该装置，鸡蛋夹放的位置离装置下端的距离x至少为多少米？（保留三位有效数字）
（1）如果没有保护，鸡蛋直接撞击地面而不被摔坏，其速度最大为鸡蛋从高度h处自由落地时的速度，
mgh=
1
2
mvm2
vm=
2
m/s
（2）装置从高度H处落到地面时，鸡蛋速度为v，
mgH=
1
2
mv2①
装置与地面作用过程中，鸡蛋从离地x处滑到地面时速度只要小于Vm就不会被摔坏，
根据动能定理得：
（mg-Ff）x=
1
2
m（vm2-v2） ②
由①②解得：x=0.433m
答：（1）如果没有保护，鸡蛋直接撞击地面而不被摔坏，其速度最大不能超过
2
m/s；
（2）如果使用该装置，鸡蛋夹放的位置离装置下端的距离x至少为0.433m．
练习册系列答案
相关题目
在一次抗洪抢险活动中，解放军某部运用直升机抢救一重要落水物体，在静止在空中的直升机上用电动机通过悬绳将物体从离飞机90m处的洪水中吊到机舱里，已知物体的质量为80kg，吊绳的拉力不能超过1200N，电动机的额定输出功率为12kW，为尽快把物体安全救起，操作人员采取的办法是：先让吊绳以最大的拉力工作一段时间，达额定功率后电动机以额定功率工作，当物体到达机舱时它达到最大速度。（g=10m/s2）
　　求：（1）落水物体刚到达机舱时的速度；
　　　　（2）这一过程所用的时间。
如图，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球；B处固定质量为m的小球，支架悬挂在O点，可绕过O点与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直，放手后开始运动.在无任何阻力的情况下，下列说法中正确的是（　　 ）

①A球到达最低点时速度为零
②A球机械能减小量等于B球机械能增加量
③B球向左摆动所能达到的最高位置应高于A球开始运动的高度
④当支架从左向右回摆时，A球一定能回到起始高度
A．①②③B．②③④C．①③④D．①②
如图所示，物体B的质量是物体A的1/2，在不计摩擦阻力的情况下，A物自高H处由静止开始下落，且B始终在同一水平面上，若以地面为零势能面，当A的动能与其势能相等时，A距地面的高度是（       ）
A．H/5B．2H/5C．4H/5D．H/3
下列说法正确的是（　　）
A．如果物体（或系统）所受到的合外力为零，则机械能一定守恒
B．做匀加速运动的物体，其机械能可能守恒
C．滑动摩擦力和静摩擦力一定都做负功
D．系统内两物体间相互作用的一对摩擦力做功的总和不一定等于零
质量为m的物体从高h处自由落下，不计空气阻力．当它下落到高度为
3
4
h处时，它的动能大小等于（　　）
A．mghB．
1
4
mgh		C．
1
2
mgh		D．
3
4
mgh
以下说法中正确的是（　　）
A．物体做匀速直线运动，它的机械能一定守恒
B．物体所受合力的功为零，它的机械能一定守恒
C．物体所受合力不等于零，它的机械能可能守恒
D．物体所受合力等于零，它的机械能可能守恒
物体由静止开始沿固定光滑斜面下滑，其末速度的大小（　　）
A．只与物体的质量有关，质量越大、速度越大
B．只与物体的质量有关，质量越大、速度越小
C．只与下滑的高度有关，高度越高、速度越大
D．只与下滑的高度有关，高度越高、速度越小
劲度系数为k的轻质弹簧，下端挂质量为m的小球，小球静止时离地面高为h，用力向下拉球使之与地面接触，而后从静止放开小球（弹簧未超过弹性限度）则（　　）
A．球在运动过程中，距地面的最大高度为2h
B．球在上升过程中弹性势能不断减少
C．球距地面高度为h时，速度最大
D．球的最大加速度为kh/m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网