题目内容
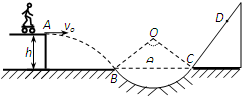
如图所示，一个小球从光滑斜面上无初速度滚下，然后进入一个半径为0.5m的光滑圆形轨道的内侧，小球恰能通过轨道的最高点，则小球下滑的高度h为______m，通过最低点时小球的向心加速度为______m/s2．（g=10m/s2）
小球恰好能通过最高点，在最高点，由重力提供向心力，设最高点的速度为v，则有：
mg=m
，
得：v=
=
m/s=
m/s
从开始滚下到轨道最高点的过程，由机械能守恒定律得：
mgh=2mgr+
mv2
联立得：h=
r=
×0.5m=1.25m
从开始滚下到轨道的过程，由机械能守恒定律得：
mgh=
mv′2，得：v′2=2gh
在最低点，小球的向心加速度为 a=
=
=
m/s2=50m/s2．
故答案为：1.25，50
mg=m
| v2 |
| r |
得：v=
| gr |
| 10×0.5 |
| 5 |
从开始滚下到轨道最高点的过程，由机械能守恒定律得：
mgh=2mgr+
| 1 |
| 2 |
联立得：h=
| 5 |
| 2 |
| 5 |
| 2 |
从开始滚下到轨道的过程，由机械能守恒定律得：
mgh=
| 1 |
| 2 |
在最低点，小球的向心加速度为 a=
| v′2 |
| r |
| 2gh |
| r |
| 2×10×1.25 |
| 0.5 |
故答案为：1.25，50
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
用如图1所示实验装置验证机械能守恒定律．水平桌面上固定一倾斜的气垫导轨，导轨上A点处有一带长方形遮光片的滑块，其总质量为m，遮光片两条竖边与导轨垂直；导轨上B点处有一光电门，测得遮光片经过光电门时的挡光时间为t，用d表示A点到导轨底端C点的距离，h表示A与C的高度差，b表示遮光片的宽度，s表示A、B两点间的距离．将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度，用g表示重力加速度．完成下列填空和作图： （1）若将滑块自A点由静止释放，则在滑块从A运动至B的过程中，滑块、遮光片组成的系统重力势能的减小量表示为△EP=______．动能的增加量表示为△Ek=______．在滑块运动过程中若机械能守恒，则与s的关系式为=______． （2）多次改变光电门的位置，每次均令滑块自同一点（A点）下滑，测量相应的s与t值，结果如下表所示：
|