题目内容
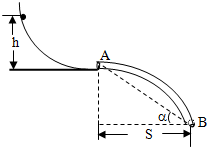
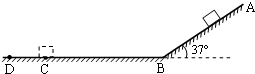
如图所示,质量m=2kg的小物块从倾角θ=37°的光滑斜面上的A点由静止开始下滑,经过B点后进入粗糙水平面,已知AB长度为3m,斜面末端B处与粗糙水平面平滑连接.试求:
(1)小物块滑到B点时的速度大小.
(2)若小物块从A点开始运动到C点停下,一共经历时间t=2.5s,求BC的距离.
(3)上问中,小物块与水平面的动摩擦因数μ多大?
(4)若在小物块上始终施加一个水平向左的恒力F,小物块从A点由静止出发,沿ABC路径运动到C点左侧3.1m处的D点停下.求F的大小.(sin37°=0.6,cos37°=0.8)
(1)小物块滑到B点时的速度大小.
(2)若小物块从A点开始运动到C点停下,一共经历时间t=2.5s,求BC的距离.
(3)上问中,小物块与水平面的动摩擦因数μ多大?
(4)若在小物块上始终施加一个水平向左的恒力F,小物块从A点由静止出发,沿ABC路径运动到C点左侧3.1m处的D点停下.求F的大小.(sin37°=0.6,cos37°=0.8)

(1)根据机械能守恒得:
mgsABsin37°=
mvB2
解得:vB=
=
m/s=6m/s;
(2)物块在斜面上的加速度为:a1=gsinθ=6m/s2,
在斜面上有:sAB=
a1t2,
代入数据解得:t1=1s.
物块在BC段的运动时间为:t2=t-t1=1.5s
BC段的位移为:sBC=
(vB+0)t2=
×6×1.5m=4.5m
(3)在水平面上,有:0-vB=a2t2,
解得:a2=
=-4m/s2.
根据牛顿第二定律有:-μmg=ma2
代入数据解得:μ=0.4.
(4)从A到D的过程,根据动能定理得:
mgsABsinθ+F(sBD+sABcosθ)-μmgsBD=0
代入数据解得:F=2.48N.
答:(1)小物块滑到B点时的速度大小为6m/s;
(2)BC的距离为4.5m;
(3)小物块与水平面的动摩擦因数为0.4;
(4)F的大小为2.48N.
mgsABsin37°=
| 1 |
| 2 |
解得:vB=
| 2gsABsin37° |
| 2×10×3×0.6 |
(2)物块在斜面上的加速度为:a1=gsinθ=6m/s2,
在斜面上有:sAB=
| 1 |
| 2 |
代入数据解得:t1=1s.
物块在BC段的运动时间为:t2=t-t1=1.5s
BC段的位移为:sBC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)在水平面上,有:0-vB=a2t2,
解得:a2=
| -vB |
| t2 |
根据牛顿第二定律有:-μmg=ma2
代入数据解得:μ=0.4.
(4)从A到D的过程,根据动能定理得:
mgsABsinθ+F(sBD+sABcosθ)-μmgsBD=0
代入数据解得:F=2.48N.
答:(1)小物块滑到B点时的速度大小为6m/s;
(2)BC的距离为4.5m;
(3)小物块与水平面的动摩擦因数为0.4;
(4)F的大小为2.48N.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目