题目内容
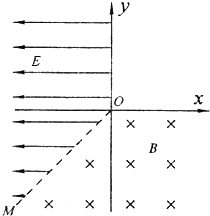
【题目】如图所示,在纸面内建立直角坐标系xOy,以第Ⅲ象限内的直线OM(与负x轴成45°角)和正y轴为界,在x<0的区域建立匀强电场,方向水平向左,场强大小E=2 V/m;以直线OM和正x轴为界,在y<0的区域建立垂直纸面向里的匀强磁场,磁感应强度B=0.1T。一不计重力的带负电粒子从坐标原点O沿y轴负方向以v0=2×103m/s的初速度射入磁场。己知粒子的比荷为q/m=5×104C/kg,求:
(1)粒子经过1/4圆弧第一次经过磁场边界时的位置坐标?
(2)粒子在磁场区域运动的总时间?
(3)粒子最终将从电场区域D点离开电,则D点离O点的距离是多少?
【答案】(1)粒子经过![]() 圆弧第一次经过磁场边界时的位置坐标为(﹣0.4m,﹣0.4m);
圆弧第一次经过磁场边界时的位置坐标为(﹣0.4m,﹣0.4m);
(2)粒子在磁场区域运动的总时间1.26×10﹣3s;
(3)粒子最终将从电场区域D点离开电场,则D点离O点的距离是7.2m.
【解析】
试题(1)粒子做匀速圆周运动,根据牛顿第二定律,求出运动的半径,从而即可求解;
(2)根据圆周运动的周期公式,可求出在磁场中总时间;
(3)粒子做类平抛运动,将其运动分解,运用运动学公式与牛顿第二定律,即可求解.
解:(1)微粒带负电,从O点射入磁场,沿顺时针方向做圆周运动,轨迹如图.
第一次经过磁场边界上的A点
由![]() ,
,
得![]() ,
,
所以,A点坐标为(﹣0.4m,﹣0.4m).
(2)设微粒在磁场中做圆周运动的周期为T,则
![]() ,
,
其中![]()
代入数据解得:T=1.256×10﹣3s
所以t=1.26×10﹣3s.
(3)微粒从C点沿y轴正方向进入电场,做类平抛运动,则
由牛顿第二定律,qE=ma
![]()
△y=v0t1
代入数据解得:△y=8m
y=△y﹣2r=8﹣2×0.4m=7.2m
即:离开电磁场时距O点的距离为7.2m.
答:(1)粒子经过![]() 圆弧第一次经过磁场边界时的位置坐标为(﹣0.4m,﹣0.4m);
圆弧第一次经过磁场边界时的位置坐标为(﹣0.4m,﹣0.4m);
(2)粒子在磁场区域运动的总时间1.26×10﹣3s;
(3)粒子最终将从电场区域D点离开电场,则D点离O点的距离是7.2m.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案